
1. Définitions.
Le bruit est généralement modélisé par une distribution de probabilité d'amplitude gaussienne. L'ensemble des valeurs instantanées d'une tension de bruit est une distribution aléatoire qui obeit au modèle simple du bruit blanc additif gaussuen (BBAG). Il est blanc car sa densité spectrale &gama; ne dépend pas de la fréquence. Il est additif car le bruit se superpose au signal indépendamment de celui-ci. Il est donc possible de mesurer le bruit en l'absence de signal. Il est gaussien car la loi de distribution de tension de bruit est une loi gaussienne à valeur moyenne nulle.
d(u) = 1/[ σ sqrt(2* π)] * exp [-u²/2 σ ²]
Figure 1 : Représentation d'une densité spectrale de bruit.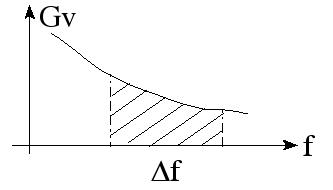 |
Densité spectrale : puissance Gv(f) en V²/Hz énergie Gv(f) en V²s/Hz. |
La densité spectrale de puissance (DSP) est le carré du module de la transformée de Fourrier du signal. La densité spectrale de puissance d'un signal est la transformée de Fourrier de sa fonction d'auto-corrélation.
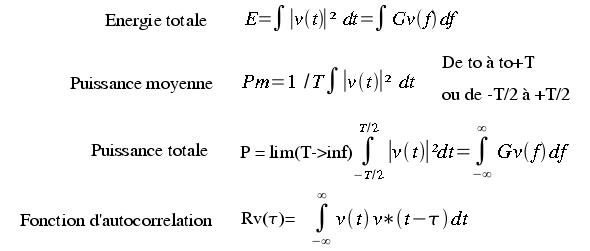
v(t) -----TF-----> V(f) Rv( &tau) <----- Gv(f)=|V(f)|²Le bruit pose un problème lors de traitement à faibles niveaux ; il apparait alors une dégradation des caractéristiques telles que la sensibilité d'un récepteur, ou plus généralement, la qualité du signal utile. Il est donc nécessaire de prendre quelques précautions afin de s'assurer que le signal reste suffisemment important par rapport au bruit.

2. Introduction.
Il éxiste deux classes de bruit :
Les bruits d'environnement d'origine non naturelle et générés de façon humaine par les moteurs, les
voitures, les apprareils ménagers, les transmissions diverses... Les protections sont possibles et du
domaine de la CEM (filtrage secteur, blindage...)
Le bruit de la matière dont l'origine est naturelle, c'est un phénomène totalement aléatoire,
imprévisible, qui utilise une description statistique.
Figure 2 : Représentation temporelle d'un bruit.

b(t) décrit le bruit de façon temporel.
b\(t) la valeur moyenne généralement nulle du bruit.
|b\|² le carré de la valeur moyenne.
b\ la composante continue DC.
[b(t)]²\ la valeur quadratique moyenne (puisance totale).
b²\ - (b\)² la puissance alternative AC ou variance.
la racine carré du truc précédent est la valeur efficace ou écart type.

3. Le bruit thermique (Johnson noise).
Le bruit thermique est trouvé en 1927 par Johnson ; en 1928 Nyquist le calcul. Il apparait une valeur efficace de bruit aux bornes d'une résistance, elle est induite par l'agitation thermique des électrons.
Figure 3 : Densité spectrale de bruit thermique.
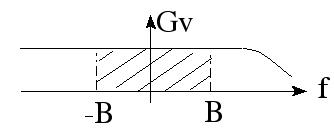
La densité spectrale du bruit thermique est constante jusqu'à 1THz environ et ne dépend que de R et T. Puissance totale dans une bande B :
P = int de -B à B de Gv(f)df = 4RkTB = 2B * 2RkT = Vb²\
Tension éfficace de bruit thermique :
Vb = sqrt (Vb²\) = sqrt(4RkTB) = 0,127 sqrt(B)
Pour T=300K dans 1 Hz en mV/sqrt(Hz)
Vb=4µV si B=1MHz et R=1k Ω

4. Le bruit de grenaille (shot noise).
Le bruit de grenaille, ou bruit Scottky est d'origine physique. il est crée au niveau d'une jonction d'un semi-conducteur, là ou existe une barrière de potentiel interne. Il résulte de la fluctuation du débit des particules à travers la jonction.
Gi(f) = q.I en A²/Hz
Valeur efficace du courant de bruit :Ish² = int de -B à B de Gi(f)df = 2q.i.B
Puissance dissipée dans R :
P = R.Ish² = 2R.q.I.B en W/Hz
P = kT = 2.R.q.I.B
Donc I=10nA pour R=1M Ω dans 1 Hz

5. Bruit BF, bruit de scintillation, bruit en 1/f.
Le bruit BF est croissant quand la fréquence diminue. Il a pour origine la dérive liée à des piégages de charge ou des défauts de surface et d'interface.
Gv(f) = k/f N avec 0,9 < N < 1,35
Gv(f) = k/f

6. Pour en finir.
Le bruit blanc est un modèle mathématique de représentation du bruit. En pratique, les sources de bruit sont indépendante, il est donc autorisé d'additionner les différentes sources de bruit : les tensions des différentes sources d'ajoutent quadratiquement.
U² = Σ (Vi) 2