et principes fondamentaux.

0. Lois de Kirchhoff.
Loi des noeuds : La somme des courants dirigés vers un noeud du circuit est égale à la somme des courants issuent de ce même noeud. (autrement dit : ce qui arrive = ce qui repart)
Loi des mailles : La somme algébrique des tensions relevées le long d'une maille est nulle ; les tensions orientées dans le sens de parcours de la maille sont comptées positivement, celles dans le sens oposé, négativement.

1. Théorème de Millmann.
Considérons les courants qui partent d'un noeud N constitué de trois branches, nous avons I1+I2+I3 = 0 ; Cette expression peut encore s'écrire, en tenant compte des impédances dans les différentes branches (cette formule peut-être adaptée pour X branches) :
(Vn-V1)/Z1 + (Vn-V2)/Z2 + (Vn-V3)/Z3 = 0 soit encore :
Vn = [V1/Z1 + V2/Z2 + V3/Z3] / [1/Z1 + 1/Z2 + 1/Z3]
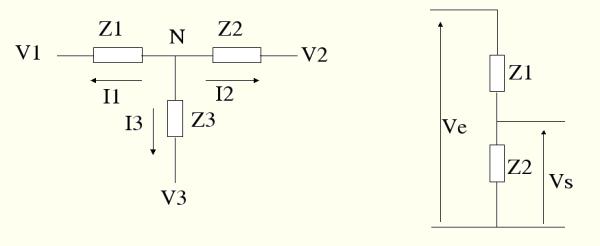
Précisons quand même la formulation du théorème de Millman : La tension en un point est le rapport de la somme des courants sur la somme des admittances. (somme des Ui/Ri de chaque branche divisé par la somme des 1/Ri de chaque branche).

2. Théorème de superposition.
Si un circuit linéaire comprend plusieurs générateurs, le courant circulant dans une branche
de ce circuit est la somme des courants qui seraient créés par chaque générateur pris isoléments,
les autres ayant été remplacés par leur impédance interne. (rappelons que l'impédance interne
d'un générateur de tension est considérée comme nulle, celle d'une source de courant comme infinie)
Une application usuelle concerne le montage à transistor ; dans un premier temps est étudié la
partie continue du circuit (polarisation) puis en second lieu, la partie alternative (amplification).

3. Théorème de Thévenin et de Norton.
Un réseau linéaire pris entre deux noeuds quelconques est équivalent à un générateur de tension Eth et de résistance interne Rth. Eth est la tension que l'on mesure entre ces noeuds quand aucune charge extérieure ne les relie (I=0 ; tension à vide aux bornes du dipôle). Rth est la résistance que l'on mesure entre ces noeuds quand on éteint les sources (Eteindre les sources revient à court-circuiter les fém et à ouvrir les générateurs de courant, les résistances internes restant dans le circuit.)
Théorème de Norton : Tout circuit électrique linéaire placé sous forme de dipôle est équivalent à un dipôle équivalent de Norton formé d'un générateur de courant parfait In et d'une résistance Rn associée en parallèle. La valeur du courant In est égal au courant entre les deux bornes court circuitées du dipôle. Rn est la résitance équivalente de l'ensemble du circuit lorsque toutes les sources de tension ont été court-circuitées et les générateurs de courant remplacés par des circuits ouverts.
Equivalence Thévenin-Norton : tout générateur de tension parfait Eth placé en série avec une résistance Rth est équivalent à un générateur de courant Eth/Rth placé en parallèle avec Rth.

4. Le diviseur de tension.
C'est une application de la traditionnelle règle de trois plus qu'un théorème ; si la tension aux bornes de deux impédances branchées en séries Z1 et Z2 est Vo , alors la tension aux bornes de Z2 est le rapport Z2/(Z1+Z2) de Vo. La démonstartion est évidente :
Vo = (Z1+Z2)*I et V2=Z2*I
V2 = Z2/(Z1+Z2) * Vo

5. Pourquoi normaliser 50 Ω au lieu de 60 ou 70 Ω ?
Extrait de EDN numéro 14 - Novembre 2000.
L'impédance des lignes de transmission sur un circuit imprimé est généralement de 50 Ω cette impédance
se retrouve dans les carctéristiques des composants et de la métrologie. C'est une valeur qui est liée à des
constantes physiques. Le champ électromagnétique proche d'une ligne est proportionnel à la hauteur de la ligne
au dessus du plan de masse : à hauteur faible correspond moins de radiation ; la diaphonie varie en fonction
de cette hauteur, la diviser d'un facteur deux conduit à une diaphonie réduite d'un facteur 4. Des faibles
hauteurs permettent d'obtenir des impédances réduites moins sensibles moins sensibles aux charges capacitives.
(d'ou la meilleure tenue aux HF d'un epoxy de 0,8 par rapport à 1,6mm).
Mais si la ligne est très proche du plan de masse, son impédance devient faible et les circuits risquent de ne
plus pouvoir fournir l'intensité pour piloter une ligne d'impédance inférieure à 50 Ω. Coté câble,
l'optimisation des constantes physiques conduit à 50 Ω l'impédance est donnée par la relation :
Zo = [60/sqrt(εr)].ln(d2/d1)
εr représente par permittivité relative du diélectrique, d1 le diamètre du conducteur interne et d2 le diamètre du conducteur externe. L'inductance s'exprime par :L # [sqrt(εr).(1+ d2/d1)] / [60.d2.ln(d2/d1]
Le tracé de la fonction représentant la valeur de l'inductance en fonction du rapport d2/d1 montre une valeur minimum pour d2/d1 = 3,5911 Le polyéthylène, matériau isolant entre la tresse et l'âme du câble à une constante diélectrique de 2,25 correspondant à une vélocité de 66% de la vitesse de la lumière. En reportant ces valeurs dans l'expression de l'impédance, on obtient une valeur de 51 Ω Les ingénieurs radio des décennies précédentes ont donc décidé de fixer de fixer l'impédance du coaxial à 50 Ω. La valeur minimum de L varie peu tant que l'on reste proche de 50 Ω. Différents diélectriques utilisés avec la meilleure valeur du rapport d2/d1 conduisent à des impédances optimales différentes.