
1. Préambule.
C'est en 1932 que De Bellescize publia sa théorie sur la détection synchronisée et décrivit la PLL
pour la première fois [La réception synchrone, Onde électrique Vol, 11 juin 1932 pp230-240].
En 1947, une réalisation à PLL était appliquée pour la première fois dans la synchronisation en
fréquence d'un récepteur télé. Dès 1970, le développement rapide des semi-conducteurs permirent
d'intégrer dans un composant un système à PLL. Ce principe est actuellement utilisé dans la plupart
des systèmes de transmission.
Généralement, les systèmes de communication sans fil nécessite l'utilisation d'une source pure,
stable et rapidement modifiable. Pour cela, la PLL corrige la différence de phase entre un signal
de référence et un signal de retour. Plusieurs techniques existent, la synthèse de fréquence directe
(DFS), la synthèse N/N+1 ou, développée plus récemment, la synthèse N fractionnée.
2. Rappel théorique sur la PLL.
La boucle à verrouillage de phase est composée d'un détecteur de phase qui calcul l'erreur de phase entre
un signal de référence et le signal pilote ; cette erreur est ensuite filtrée par un filtre de boucle
(filtre passe bas) avant d'entrer sur la commande d'un VCO.
Le détecteur de phase influence sur la dynamique et la performance de la PLL. Plusieurs comparateurs de
phase existent ; le comparateur dit « charge pump », par exemple, utilise deux bascules D puis des buffers
qui convertissent l'état logique du détecteur de phase en courant permettant de commander le VCO via un filtre
de boucle. Le filtre de boucle est un élément important d'un système à PLL qui relie le détecteur de phase au VCO.
Généralement un filtre passif est utilisé du fait de sa simplicité, de son faible coût et de ses performances
en bruit de phase.

2.1 Le comparateur de phase.
Le comparateur de phase délivre une tension dont la valeur moyenne est proportionnelle à la différence de
phase des signaux d'entrées. Le détecteur de phase peut-être analogique (mélangeur doublement équilibré,
multiplieur 4 quadrants) ou numérique (porte ou exclusif, logique séquentielle...).
Kd = Du/Dphi représente le gain du détecteur de phase en Volt/rad.
2.1.1 Mélangeur / multiplieur
Le multiplieur analogique linéaire peut prendre différentes formes, selon l'application;
soit un multiplieur quatre quadrants à cellules de Gilbert, soit une structure à diode pour
les fréquences plus élevées...
v_1 = Ua cos(w1t)
v_2 = Ub cos(w1t + PHI)
or sin(a) * sin(b) = 0.5 * cos(a-b) - 0.5 * cos(a + b)
Vd = (k * Ua * Ub / 2) * [cos(PHI) - cos(2w+PHI)]
Vd # (k * Ua * Ub / 2) * cos(PHI) après filtrage passe bas.
2.1.2 Ou exclusif.
Les détecteurs de phase numériques requièrent des signaux carrés sur leurs entrées et permettent un verrouillage plus facile que dans le cas précédent lors d'écart entre le signal utile et le signal de référence. La porte OU exclusif constitue le comparateur le plus simple.
___ ___ __ ____
Pour Phi=0, u=0V ___| |___| |___| a ___| | a b S
_ ___ ___ |XOR |___S 0 0 0
Pour Phi=Pi/2, u=Vdd/2 |___| |___| |___| b ___| | 0 1 1
_ _ _ _ _ _ |____| 1 0 1
Pour Phi=Pi, u=Vdd |_| |_| |_| |_| |_| |_ 1 1 0
Le point de verrouillage à fréquence centrale s'effectue à Vdd/2.Kd = (Logic'1' - Logic'0') / PI
2.1.3 Détecteur de phase séquentiel.
Le circuit de base utilise une bascule RS déclenchée sur front, on trouve des variantes utilisant une ou plusieurs bascules D ou JK.

La sortie Q est mise à l'état haut avec un front descendant sur u1 (set), le passage de la sortie à l'état bas s'effectuant sur un front descendant de u2 (reset). Du fait du déclenchement du montage sur un front du signal, ce principe est indépendant du rapport cyclique. Contrairement au cas précédent, ce système est indépendant du rapport cyclique des signaux d'entrée. Par contre, pour des fréquences d'entrées verrouillées sur f1 et f2 assez proche, la valeur de sortie ne se stabilise pas et évolue à une période égale à la différence des deux fréquences.
Kd = (Logic'1' - Logic'0') / 2.PI
2.1.4 Comparateur phase/fréquence séquentiel (PFD).
Le détecteur phase/fréquence donne une information à la fois sur la phase, mais aussi sur la fréquence.
Une information de phase est fournie pour une erreur de +/- 2PI radians.
Exemple de réalisation & principe :
Le PFD compare le signal de référence Fref avec le signal divisé provenant du VCO et active des sorties UP
et DOWN selon la différence de phase entre ces deux signaux. Quand la différence de phase est supérieure à
2.PI, le circuit est dans un mode de détection de fréquence, la sortie de courant délivre alors une valeur
constante (cas d'un circuit charge pump). Le filtre de boucle intègre cette valeur et le PFD continue d'opérer
jusqu'à ce que l'erreur entre les deux signaux d'entrée passe en dessous de 2.PI ; le circuit opère alors en
mode détection de phase ; dès que la différence de phase approche zéro, le circuit entre dans un état verrouillé.
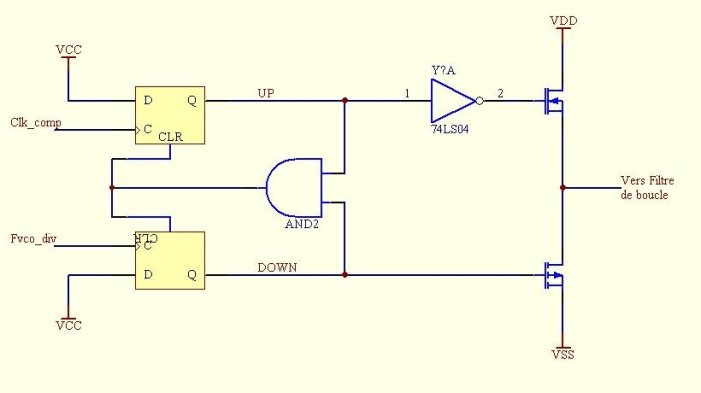 Description VHDL du comparateur de phase :
Description VHDL du comparateur de phase :
process(Clk_comp,aRST,Reset)
begin
if(aRST='1' or reset='1') then
Q_up <= '0';
elsif rising_edge(Clk_comp) then
Q_up <= '1';
end if;
end process;
process(Fvco_div,aRST,Reset)
begin
if(aRST='1' or reset='1') then
Q_down <= '0';
elsif rising_edge(Fvco_div) then
Q_down <= '1';
end if;
end process;
reset <= Q_up and Q_down;
PHiD_P_pdh <= '0' when (PhiD_down_pdh='1') else 'Z';
PHiD_M_pdh <= '1' when (PhiD_up_pdh='1') else 'Z';
La sortie UP vaut '1' et DOWN vaut '0' si le signal du VCO est trop faible en fréquence. (erreur de phase positive)
UP est positionné à '1' à chaque front montant de clk_comp et positionné à '0' quand up et down vallent '1'.
La sortie DOWN vaut '1' et UP vaut '0' si le signal du VCO est trop haut en fréquence. (erreur de phase négative)
DOWN est positionné à '1' à chaque front montant de Fvco_div et positionné à '0' quand up et down vallent '1'.
L'erreur de phase généreré des variations autour de la fréquence centrale jusqu'à stabilisation, la PLL sera alors
verrouillée, il n'y a aura plus d'erreur de phase et les deux sorties UP et DOWN seront à '0'.
Kd = (Logic'1' - Logic'0') / 2.PI
2.1.5 Circuit à pompe de charge. (charge pump)
Le comparateur « charge pump » est identique au détecteur phase/fréquence mise à part qu'il dispose d'une unique sortie de courant au lieu de deux en tension. On ajoute donc deux buffer de courant en sortie du montage précédent. (généralement des transistors MOS comme représenté sur le montage ci-dessus) Souvent le courant de sortie est programmable permettant des consommations plus faibles du circuit d'intégration qui suit. Cet intégrateur génère, à partir du courant, une tension qui pilote le VCO ; de ce fait, un faible courant du détecteur augmente les impédances de l'intégrateur alors qu'un courant élevé diminue le niveau des impédances.Kd = (Imax/2.PI) en Amp/rad
2.2 Le filtre passe bas.
Le signal de sortie du comparateur de phase est constitué d'harmonique et d'une composante continue. Le rôle du filtre passe bas est de ne conserver que cette composante continue qui est proportionnelle à l'écart de phase. Souvent un filtrage trop peu rigoureux laisse passer des résidus de la fréquence de comparaison que l'on peut retrouver ensuite en pied de porteuse.

1/(1+RCp)
(1+R2Cp)/(1+R1Cp+R2Cp)
(1+R2C1p)/(1+R1C1p+R2C1p+R1C2p+R1R2C1C2p²)
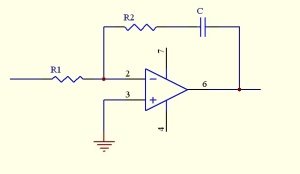
(1+R2Cp)/(R1Cp)
(1/R1C2p)(1+R2C2p)/(2+R1C1p) (à confirmer avec spice)
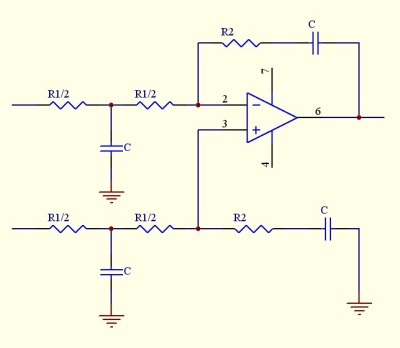
2.3 Le VCO.
Il peut être de plusieurs type :
Soit un oscillateur à circuit accordé : LC avec varicap.
Oscillateurs RF à transistors.
Soit à quartz, dans ce cas l'excusrion est faible.
Oscillateurs à quartz.
Ou à résonnateur diélectrique (hyper fréquence par exemple).
Oscillateur à résonnateur diélectrique.
Le VCO est généralement conçu de façon à obtenir une réponse linéaire ; on le carctérise par
son gain Kvco = Df/Dv en MHz/V.
3. Tableau récapitulatif des fonctions de transferts.
4. Caractérisation de la pll, calcul des éléments.
4.1 Notions mathématiques : transformée de Laplace.
Transformation de Laplace. (pierre Simon Laplace, mathématicien (1749-1827).
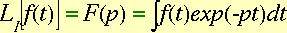

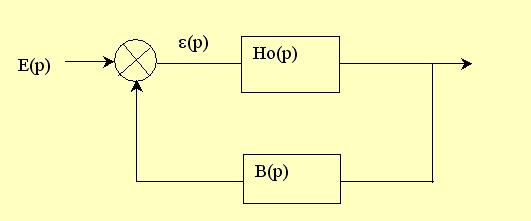
Ho(p) = la fonction de transfert de la chaine direct.
B(p) = la chaine de retour.
Ho(p).B(p) = fonction de transfert de la boucle ouverte.
Ho(p)/(1+Ho(p).B(p)) = fonction de transfert de la boucle fermée. (Formule de Black)
4.2 Système en boucle ouverte.
Quelques considérations d'ordre général.
L'Ordre de la PLL = ordre du filtre de boucle + 1.
L'état de verrouillage doit être obtenu avec un temps de réponse rapide.
Plage de capture : la synthèse peut récupérer toute dérive de phase.
Plage de verrouillage : c'est la plage d'utilisation normale d'une PLL. (inférieur à plage de capture).
La fonction de transfert en boucle ouverte permet de définir les éléments du filtre de boucle.
La stabilité du système est définit par la marge de phase.
BO(p) = (Kvco / p) * (Kd / N) * F(p).
MP = 180° - arg Ho(p) = 45°
4.3 Système en boucle fermée.
Soit Ho(p) la fonction de transfert de la chaîne directe,BF(p) = Ho(p) / ( 1 + B(p)*Ho(p)).
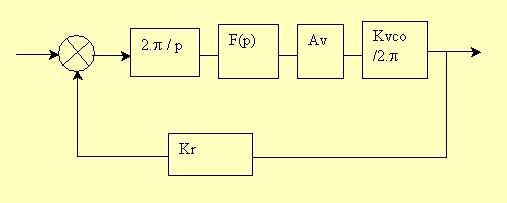
Note concernant le bruit de phase :
Le bruit de phase de la sortie synthétisée est déterminé par le bruit du quartz de référence, ensuite
par le bruit du détecteur de phase et ce jusqu'à la bande passante du filtre, puis par le VCO.
Les bruits ramenés par le cristal et le détecteur de phase sont dégradés de 20logN à l'intérieur de la
bande passante du filtre de boucle, mais filtré par sa fonction de transfert au delà. Le bruit du VCO
est considérablement atténué pour des fréquences proches de la porteuse alors que le bruit sera transmis
sans atténuation à des fréquences avoisinants le filtre de boucle et au delà. L'augmentation de l'ordre
du filtre de boucle de 2 à 3 ou 4 permet une meilleure atténuation des éléments parasites et du bruit.
Une faible largeur de bande du filtre de boucle améliore le bruit de phase pour des offsets fm supérieurs
à la largeur du filtre ; une plus haute largeur de bande améliorera le bruit proche et à l'intérieur de
la bande.
Généralement le bruit de phase est induit par le VCO, Le coéfficient de charge Q du VCO est un
élément primordial dans la détermination du bruit de phase.
5. Modélisation sous Mathlab.
Exemples pratiques et calcul des éléments avec mathlab.
La partie numérique de la PLL est détaillée en fin de document.
Figure 1 : schéma de la pll.
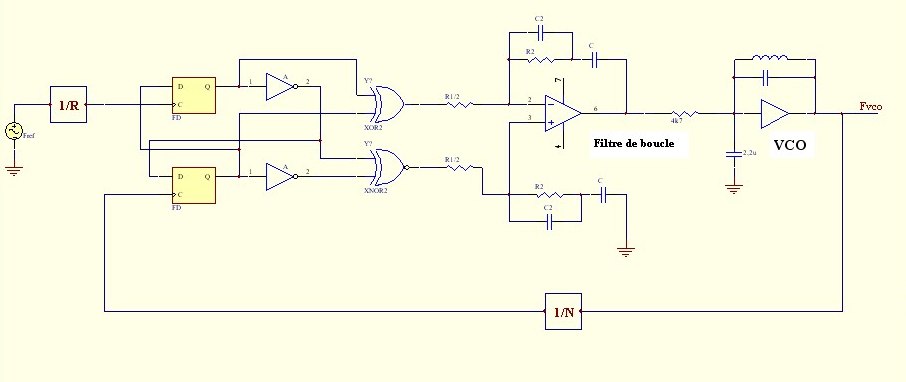
Les valeurs suivantes seront utilisées pour les calculs :
Kpd = 9 Volts / 2*pi = 1,432 Volts/rad
Kvco = 2*pi* (2*125ppm) *44,736MHz = 17,27e3 rad/Volt.sec
Présentation du script de calcul de stabilité sous mathlab :
%------------------------------------------------------------------------------- %-- Titre : boucle à verrouillage de phase %-- Projet : X_OC3 %------------------------------------------------------------------------------- %-- Fichier : pll %-- Auteur : FLP/OTT %-- Compagnie : OTT %-- Création : 05/11/2003 %-- Last update: -- %------------------------------------------------------------------------------- %-- Description : Modélisation d'une pll... %-- terminologie : Dans la suite du document, Ho représente la fonction de % transfert de la chaine directe & B, la boucle de retour. % Le sigle FT désigne la Fonction de Transfert. % BO & BF respectivement Boucle Overte & Boucle Fermée. %-- Définition : Transformée de laplace : H(p) = INT [H(t)exp(-p*t)dt] % : Transformée inverse : h(t) = (1/2*pi*j) INT [F(p)exp(p*t)dp] %-------------------------------------------------------------------------------
close all
clear all
clc
%-------------------------------------------------------------------------------
% Paramètres globaux.
%-------------------------------------------------------------------------------
fe = 10000;
N = 6192;
t = 0:1/fe:2; %nb d'éléments de la matrice : 20 000(2*fe)
%-------------------------------------------------------------------------------
% Filtre de boucle seul.
%-------------------------------------------------------------------------------
% Rappel sur la fonction freqs :
% soit H(p) =(0.2 * p^2 + 0.3 * p + 1) / (0.4 * p + 1)
% a = [0.4 1] et b = [0.2 0.3 1]
% Par la suite, la fonction freqs sera utilisé pour représenter la FT.
%-------------------------------------------------------------------------------
% Filtre de boucle passif d'ordre 1 (R1+C) : (a)
% H(p) = 1 / (1 + Tau1 * p)
% Filtre de boucle passif d'ordre 1 modifié (R1+R2/C) : (b)
% H(p) = (1 + Tau2 * p) /(1 + (Tau1 + Tau2) * p)
% Filtre de boucle actif d'ordre 1 :(c)
% H(p) = (1 + Tau2 * p) / (Tau1 * p)
% Filtre de boucle actif avec intégrateur :(d)
% H(p) = K/p * (p+z1) / (p+p1)
% Filtre de boucle actif 'c' modifié :(e)
% H(p) = (1/Tau11*p) * (1 + Tau22*p)/(2 + Tau11*p)
%-------------------------------------------------------------------------------
string_name_lpf = 'Fonction de transfert du filtre de boucle';
w = logspace(-2,4);
f = w/(2*pi); % conversion de la pulsation en fréquence
% paramètres du filtre de boucle (d)
% extrait de la documentation TranSwitch.
% On choisit z1=0.1 et p1=10
% le passage à 0 du gain sera analysé avec la FT en BO
Rin = 1000e3; % N'influence pas les points d'inflexions, juste le gain.
Cs = 10e-6; %diminuer Cs pour avoir un gain nul à l'optimum de phase.
Rf = 1e6;
Cp = 100e-9;
Tau11 = Rin*Cs;
Tau22 = Rf*Cp;
Tau21 = Rf*Cs;
K = (Tau21+Tau22)/(Tau11*Tau22);
zero1 = 1/(Tau21+Tau22);
pole1 = 1/Tau22;
a_d = [1 pole1 0]; %polynome du dénominateur
b_d = [0 K K*zero1]; %polynome numérateur
H_lpf_d = freqs(b_d,a_d,f)
mag_d = abs(H_lpf_d);
phase_d = angle(H_lpf_d);
magdB_d = 20*log10(mag_d); %conversion de la magnitude en décibel
phaseDeg_d = phase_d*180/pi; %conversion de la phase en degrés.
% paramètres du filtre de boucle (c)
% l'ordre du dénominateur est identique à celui du numérateur;
% qd la fréquence est importante, le gain tend vers R2/R1
% et peut ne jamais descendre en dessous de 0dB...
R1 = 33e3;
R2 = 3.3e3;
C = 2.2e-6;
Tau1 = R1*C;
Tau2 = R2*C;
a_c = [Tau1 0]; %polynome du dénominateur
b_c = [Tau2 1]; %polynome numérateur
H_lpf_c = freqs(b_c,a_c,f)
mag_c = abs(H_lpf_c);
phase_c = angle(H_lpf_c);
magdB_c = 20*log10(mag_c); %conversion de la magnitude en décibel
phaseDeg_c = phase_c*180/pi; %conversion de la phase en degrés.
% paramètres du filtre de boucle (e)
% Utilisation sur la carte OTA gigue.
R1in = 4.7e3;
C1in = 100e-9;
R2cr = 33e3;
C2cr = 2.2e-6
R2neg = 1e6; %n'influence pas la stabilité : diminue la gain static.
C2pos = 10e-9; %non connecté : introduit un pôle instable.
Tau22_e = R2cr*C2cr;
Tau11_e = R1in*C1in;
Tau12_e = R1in*C2cr;
a_e = [Tau12_e*Tau11_e 2*Tau12_e 0]; %polynome du dénominateur
b_e = [0 Tau22_e 1]; %polynome numérateur
H_lpf_e = freqs(b_e,a_e,f)
mag_e = abs(H_lpf_e);
phase_e = angle(H_lpf_e);
magdB_e = 20*log10(mag_e); %conversion de la magnitude en décibel
phaseDeg_e = phase_e*180/pi; %conversion de la phase en degrés.
subplot(2,1,1), semilogx(f, magdB_d), xlabel('fréquence'), ylabel('magDB'), title(string_name_lpf)
grid on;
subplot(2,1,2), semilogx(f, phaseDeg_d), xlabel('fréquence'), ylabel('phase')
grid on;
pause;
%-------------------------------------------------------------------------------
% Modélaisation de la PLL.
%-------------------------------------------------------------------------------
% Décomposition de la pll en éléments simples.
% Définition des paramètres d'entrée.
%-------------------------------------------------------------------------------
Val_N = 512; %coef de division N de la PLL
PreDiv = 32; %facteur de prédivision
Val_R = 16384; %facteur de division R de la PLL
K_phi = 3.3/(2*pi); %gain du comparateur de phase
K_vco = 2*pi*(10e3/3); %gain du vco=delta_f/delta_v (écart de fréquence/écart de tension)
Av = 1; %gain en tension ds le cas de filtre de boucle actif
%-------------------------------------------------------------------------------
% Asservissement de la boucle à verrouillage de phase.
% On entre dans le comparateur de phase :
% la fréquence de comparaison = fref/Val_R
% et la fréquence du VCO divisée : Fvco/Val_N (ramenée au environ de fref)
% L'erreur de phase sert de tension de commande au VCO...
%-------------------------------------------------------------------------------
pulsation = logspace(-1,3);
freq = pulsation/(2*pi); % conversion de la pulsation en fréquence
K_retour = 1/(PreDiv*Val_N);
K_num = K_phi*K_vco*Av;
Alpha = K_num*K_retour;
%-------------------------------------------------------------------------------
%la fonction de transfert en BO permet de définir la marge de phase et donc la
%stabilité du système. Pour module de (H*B)=1 (gain nul en dB) il faut une marge
%de phase PHI minimale de 45° ie. PHI_Hbo > 135°
%Une marge de phase de phase de 45° correspond à un coef d'amortissement khi=0.5
%La pll est d'autant plus stable que K_num est grand, Tau1 élevé et Tau2 faible...
%Pour le filtre de boucle (d) (TranSwitch application notes)
%H_lpf(p) = K/p * (p+z1) / (p+p1)
%Le rapport Rin/Rf définit le gain choix de Rin pour l'optimum de phase.
%-------------------------------------------------------------------------------
a_bo_d = [1 pole1 0 0]; %polynome du dénominateur
b_bo_d = [0 0 K*Alpha K*Alpha*zero1]; %polynome numérateur
H_bo_d = freqs(b_bo_d,a_bo_d,freq) %calcul en fct de pulsation
magBO_d = abs(H_bo_d);
phaseBO_d = angle(H_bo_d);
magdB_BO_d = 20*log10(magBO_d); %conversion de la magnitude en décibel
phaseDeg_BO_d = phaseBO_d*180/pi; %conversion de la phase en degrés.
%avec H_lpf(p)=(1+Tau2*p)/Tau1*p on obtient
%H_bo(p) = H_lpf(p) * Kphi * Kvcxo * Av * (1/32*N) * (1/p)
a_bo_e = [Tau12_e*Tau11_e 2*Tau12_e 0 0]; %polynome du dénominateur
b_bo_e = [0 0 Alpha*Tau22_e Alpha]; %polynome numérateur
H_bo_e = freqs(b_bo_e,a_bo_e,freq) %calcul en fct de pulsation
magBO_e = abs(H_bo_e);
phaseBO_e = angle(H_bo_e);
magdB_BO_e = 20*log10(magBO_e); %conversion de la magnitude en décibel
phaseDeg_BO_e = phaseBO_e*180/pi; %conversion de la phase en degrés.
string_name_BO = 'Fonction de transfert en Boucle Ouverte';
subplot(2,1,1), semilogx(freq, magdB_BO_d), xlabel('fréquence'), ylabel('magDB'), title(string_name_BO)
grid on;
subplot(2,1,2), semilogx(freq, phaseDeg_BO_d), xlabel('fréquence'), ylabel('phase')
grid on;
pause;
%-------------------------------------------------------------------------------
%calcul de la fonction de transfert en boucle fermée :
%On utilise la formule de BLACK pour la fonction de transfert en BF.
%Formule de Black = (Boucle directe)/(1 + boucle directe * boucle Retour);
%avec H(p)=(1+Tau2*p)/Tau1*p la FT en BF est définit par :
%(Tau2*p + Kn)/(Tau1*p^2 + Tau2*p + Kd)
%On obtient la bande passante du système (freq de coupure à 3dB)
%ainsi que le facteur d'amortissement.
%-------------------------------------------------------------------------------
%Pour le filtre de boucle (d) (TranSwitch application notes)
%H_lpf(p) = K/p * (p+z1) / (p+p1)
Alpha_d = K_phi*Av*K_vco;
K_retour_d = 1/(PreDiv*Val_N);
K_direct_d = 1/(Val_R);
%denom_d = [1 pole1 K*Alpha_d*K_retour_d K*Alpha_d*K_retour_d*zero1]; %polynome du dénominateur
%numerat_d = [0 0 K*Alpha_d/Val_R K*Alpha_d*zero1/Val_R]; %polynome numérateur
denom_d = [1 pole1 K*Alpha_d*K_retour_d K*Alpha_d*K_retour_d*zero1]; %polynome du dénominateur
numerat_d = [0 0 K*Alpha_d*K_direct_d K*Alpha_d*zero1*K_direct_d]; %polynome numérateur
H_black_d = freqs(numerat_d,denom_d,freq) %fonction de transfert en BF.
magHb_d = abs(H_black_d);
phaseHb_d = angle(H_black_d);
magdB_BF_d = 20*log10(magHb_d); %conversion de la magnitude en décibel
phaseDeg_BF_d = phaseHb_d*180/pi; %conversion de la phase en degrés.
string_name_bf = 'Fonction de transfert en BF';
subplot(2,1,1), semilogx(freq, magdB_BF_d), xlabel('fréquence'), ylabel('magDB'), title(string_name_bf)
grid on;
subplot(2,1,2), semilogx(freq, phaseDeg_BF_d), xlabel('fréquence'), ylabel('phase')
grid on;
pause;
%-------------------------------------------------------------------------------
%La fct de transfert en BF permet aussi de définir la réponse à un échelon.
%La réponse à un échelon, permet de déterminer le facteur d'amortissement (khi)
%et la pulsation naturelle (wn) (tout comme la FT en BF le faisait aussi.)
%Elle se calcul en définissant S(p) = e(p)*H_bf(p)
%avec E(p)=1/p, et H_bf(p) la fct de transfert définit ci-dessus.
%En pratique, on doit calculer S(p) puis on effectue une transformée
%de laplace inverse pour retourner dans le domaîne temporel.
%Pour cette simulation, l'utilisation de la transformée en z s'avère plus simple.
%Le passage
%-------------------------------------------------------------------------------
La suite du script devait représenter la réponse à un échelon et à une rampe...
Figure 2 : fonction de transfert du filtre de boucle.
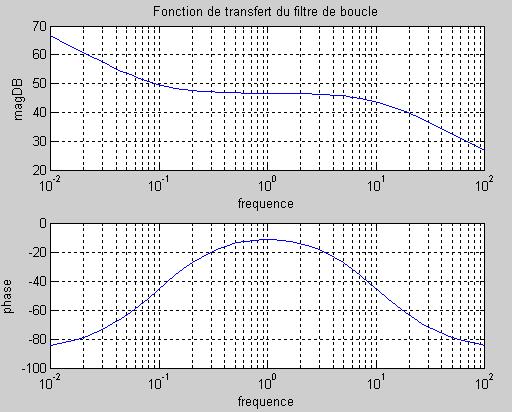
Il est courant de présenter la fonction de transfert du filtre de boucle sous sa forme pôlinomiale faisant apparaître les pôles et les zéros. Les pôles de la fonction de transfert correspondent à des changements introduisant de l'atténuation et une augmentation de phase. Les zéros de la fonction de transfert, au contraire, réduisent la phase et l'atténuation. Pour ce filtre de boucle ci-dessus, la fonction de transfert vaut :
L_lpf(p) = (K / p) * (p+ z1) / (p+p1)
K = 1 / (R1 * C2)
p1 = R1 * C1
z1 = R2 * C2
La fonction de transfert en boucle ouverte est définit par la multiplication de la chaine directe avec la chaine de retour, soit Kpd * Kvco * L_lpf(p) * 1/(N*p) La marge de phase est mesurée et ajustée avec les éléments R et C du filtre de boucle ; Une marge de phase d'environ 135° entraine une réponse trensitoire oscillante. Une marge de phase de 90° génère des pics de jitter. Une marge de phase de 45° correspond à un coefficient d'amortissement de 0,5 et un dépassement de 20% pour une entrée en échelon.
Figure 3 : Fonction de transfert en boucle ouverte.

Considérations :
La fréquence de comparaison présente à la sortie du détecteur de phase est atténuée par le filtre
de boucle. Il reste toutefois souvent un résidu présent à l'entrée du VCXO qui module la fréquence
générée et cause du buit de phase (jitter).
Un pôle suipplémentaire (RC) est donc ajouté derrière le filtre de boucle ; il ne doit pas
compromettre ni influencer la stabilité du système.
Valeur classique utilisées : R=4k7 et C=2,2uf soit une fréquence de coupure de 15Hz.
Rmax ne doit pas dépasser 1/10 de l'impédance d'entre du VCXO.
Rmin de 1k est conseillée afin de rendre le circuit RC indépendant du filtre de boucle.
Figure 4 : Fonction de transfert en boucle fermée.
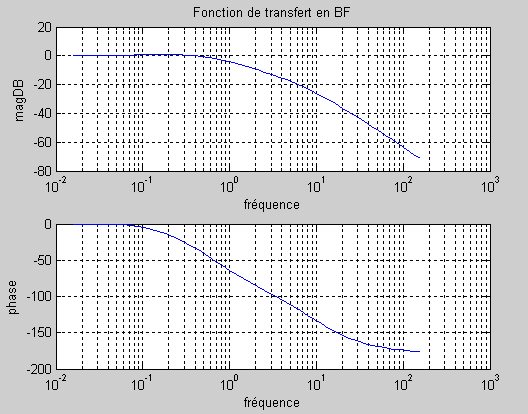
6. Glossaire.
Page de verrouillage :
Correspond à l'écart de fréquence par rapport à la fréquence centrale à partir duquel la pll se
déverrouille. (aussi appelé plage de maintien ou de poursuite)
Plage de capture :
La plage de capture correspond à l'écart de fréquence par rapport à la fréquence centrale à partir
duquel la pll se verrouille. Elle est inférieure à la plage de verrouillage et vaut de façon très
approchée, la bande passante du filtre.
TCXO : Oscillateur à quartz compensé en température.
Spurious attenuation : valeur de filtrage par le filtre de boucle de la fréquence de comparaison.
Spectrum analyser : équipement permettant de mesurer la répartition fréquentielle des puissances.
Prescaler : prédiviseur HF. (intègre une partie de N)
Overshoot : Représente le dépassement sur une réponse à un échelon d'un second ordre.
Natural frequency (ωn) : correspond à la fréquence des oscillations de la réponse à un échelon.
Fonction de transfert en BO : Kvco * Kpd * Hlpf(p) / (N * p)
PLL N dfractionnée : PLL dont le coefficient N peut être fractionnaire.
Fréquence de comparaison : Valeur du quartz divisée par R.
7. Documentation, bibliographie.
Boucle à verrouillage de phase,
Description de la partie numérique de la PLL en vhdl.
(ce ne sont que deux compteurs et un comparateur de phase.)
--
-- Asservissement de fréquence, partie numérique.
-- division par R de l'horloge de référence, on obtient clk_comp = Fref/R
-- division par K de l'horloge utile, on obtient Clk_in/K
-- L'asservissement permet d'avoir Fref/R = Fin/K soit, Fin=K*fcomp
--
-- Structure du comparateur de phase : Phase Frequency Detector.
-- gain : Kpd = (Voh-Vol)/2*PI en [V/rad]
--
library IEEE;
use IEEE.Std_logic_1164.all;
use IEEE.Numeric_std.all;
entity PLL_interne is port (
XGSR : in std_logic; -- Reset asynchrone, programmation des xilinx
CLK_in : in std_logic; -- Horloge à asservir
Clk_ref : in std_logic; -- Horloge de référence
PLL_Val_R : in std_logic_vector(10 downto 0); --facteur de division sur Fref
PLL_val_K : in std_logic_vector(15 downto 0); -- facteur de division sur Fvco
PhiD_down : out std_logic; -- sortie comparateur de phase vers LPF
PhiD_up : out std_logic; -- sortie comparateur de phase vers LPF
IO_test : out std_logic_vector(15 downto 0));
end PLL_interne;
architecture Alpha of PLL_interne is
-- compteur R-N
signal Cpt_clk_in : unsigned(15 downto 0);
signal Cpt_clk_ref : unsigned(10 downto 0);
-- division par 2 pour rapport cyclique de 50%:
signal PLL_Val_R_2 : std_logic_vector(10 downto 0);
signal PLL_val_K_2 : std_logic_vector(15 downto 0);
-- horloge de comparaison Fref/R
signal Clk_comp : std_logic;
-- horloge d'entrée divisée par K
signal Fin_div : std_logic;
-- comparateur de phase
signal Q_up : std_logic;
signal Q_down : std_logic;
signal Reset : std_logic;
begin
IO_test(7 downto 0) <= Clk_comp & Fin_div & Q_up & Q_down & Clk_ref & CLK_in & "11";
IO_test(15 downto 8) <= (others => '1');
PLL_Val_R_2 <= '0' & PLL_Val_R(10 downto 1);
PLL_Val_K_2 <= '0' & PLL_Val_K(15 downto 1);
--
-- Horloge de référence divisée par R
-- pour génération de l'horloge de comparaison
--
div_clk_comp: process(Clk_ref,XGSR)
begin
if (XGSR='1') then
Cpt_clk_ref <= (others => '0');
Clk_comp <= '0';
elsif rising_edge(Clk_ref) then
if (Cpt_clk_ref = unsigned(PLL_Val_R)-1 ) then
Cpt_clk_ref <= (others => '0');
else
Cpt_clk_ref <= Cpt_clk_ref + 1;
end if;
if (Cpt_clk_ref=0) then
Clk_comp <= '0';
elsif (Cpt_clk_ref = unsigned(PLL_Val_R_2)) then
Clk_comp <= '1';
end if;
end if;
end process div_clk_comp;
--
-- Horloge à asservir divisée par K
-- pour se rapporter à la même fréquence que clk_comp
-- à l'asservissement (phase) près
--
div_clk_in: process(CLK_in,XGSR)
begin
if (XGSR='1') then
Cpt_clk_in <= (others => '0');
Fin_div <= '0';
elsif rising_edge(CLK_in) then
if (Cpt_clk_in = unsigned(PLL_Val_K)-1 ) then
Cpt_clk_in <= (others => '0');
else
Cpt_clk_in <= Cpt_clk_in + 1;
end if;
if (Cpt_clk_in=0) then
Fin_div <= '0';
elsif (Cpt_clk_in=unsigned(PLL_Val_K_2)) then
Fin_div <= '1';
end if;
end if;
end process div_clk_in;
--
-- Comparateur de phase séquentiel
-- détecteur Phase/fréquence
--
-- Si les sorties up et down sont à '1' simultanément, les bascules sont remises à zéro (reset)
-- Deux cas possibles :
-- Si le front de Fref précède fo
-- Le premier front de fref active up, le front suivant de fo activera down et déclenchera reset
-- On obtient sur up une pulse de la durée de l'écart entre fref et fo.
-- Si Fo arrive en premier (précède fref) la pulse apparaitra sur down.
-- Le gain de cette structure est définit par Kd = (Voh-Vol)/2*PI en [V/rad]
process(Clk_comp,XGSR,reset)
begin
if (XGSR='1' or reset='1') then
Q_up <= '0';
elsif rising_edge(Clk_comp) then
Q_up <= '1';
end if;
end process;
process(Fin_div,XGSR,reset)
begin
if (XGSR='1' or reset='1') then
Q_down <= '0';
elsif rising_edge(Fin_div) then
Q_down <= '1';
end if;
end process;
Reset <= Q_up and Q_down;
PhiD_down <= Q_down;
PhiD_up <= Q_up;
end Alpha;