
1. Lignes de transmission, définitions.
Une ligne de transmission peut-être modélisée par une suite de tronçons élémentaires de longueur dx et constitué des quatre éléments R/L/C/G. Une ligne de transmission peut aussi bien être un câble coaxial qu'une ligne microstrip...
Figure 1 : Schéma équivalent d'une ligne de transmission.
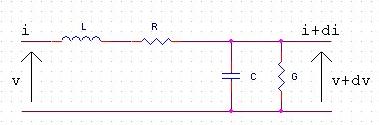
R représente la résistance lineique en Ω/m. Elle traduit les pertes par effet
joule ainsi que le rayonnement qui croit quand la fréquence augmente. R est considéré comme
constant sur Δf donné.
G correspond à la conductance lineique et résulte de l'imperfection de l'isolement des
conducteurs.
L est l'inductance lineique provenant de la mutuelle inductance présent entre deux conducteurs.
C est la par unité de longueur liée au diélectrique présent entre le signal et sa référence.

2. Mise en équation.
Considérons une ligne de longueur l et alimentée par un générateur haute fréquence tel que l>>λ. La ligne est fermée par Zr, i et u varient le long de cette ligne qui ne peut être considérée comme un court circuit. De même E et H varient.
(1) δV/δx = -R.i - L.δi/δt
(2) δi/δx = -G.v - C.δv/δt
δ²v/δx² - (RC+LG)δv/δt - LCδ²v/δt² -RGv = 0
En régime harmonique, v(x) = V(x) exp(jωt) et δ/δt = jω
δ²v/δx² - (R+jLω)(G+jCω).v = 0
δ²v/δx² - γ²(ω).v = 0
avec γ complexe de la forme α+j.β
v = v1exp(-γx) + v2exp(γx)
i = i1exp(-γx) + i2exp(γx)
δv/δx = -γ.v1.exp(-γx) + γ.v2.exp(γx) = -I(R+jLω)
=> I = sqrt[(G+jcω)(R+jLω)].[v1.exp(-γx) - v2.exp(γx)]
Soit : I = I+exp(-γx) - I- exp(γx)
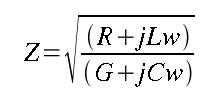
Donnons une expression approchée pour deux cas, sachant que l'on aura toujours G très inférieur
à Cω. Si L.ω est très inférieur à R, alors α=β=sqrt(R.C.ω/2) ; il y
a donc distorsion d'amplitude et de temps de propagation de groupe. Par ailleurs, l'impédance
caractéristique est complexe et non constante. Ce cas correspond aux câbles à fortes pertes (donc
R élevé) mais aussi aux fréquences faibles.
Si L.ω est très supérieur à R, alosr α=(R/2)sqrt(C/L)+(G/2)sqrt(L/C) et β=ω.sqrt(LC)
il n'y a pas de distorsion de temps de propagation de groupe; En hautes fréquences, l'atténuation
augmente avec f suivant une loi en racine de f à cause de l'effet de peau puis en f à cause de G qui
devient prépondérant.
Afin de se placer dans la deuxième condition sur les paires téléphoniques basses fréquences, on place
à intervalles réguliers de fortes inductances localisées : c'est le procédé de pupinisation. Il n'y a
alors plus de distorsion en basses fréquences tant que la longueur d'onde reste grande devant la
distance entre inductances.
v(x,t) = V1exp(jωt-γx) + V2exp(jωt+γx)
i(x,t) = [V1exp(jωt-γx) + V2exp(jωt+γx)]/(1/Zc)
v(x,t) est la somme de deux ondes progressives, une onde incidente et une onde réfléchie.
Le terme exp(-γx) correspond à l'affaiblissement en dB/m
α est le facteur d'amortissement ou atténuation lineique en Neper/m.
β correspond à la constante de phase ou déphasage lineique en rd/m
&beta=2π/λ variation de la phase de l'onde par rapport à l'origine.
Soit encore vφ = ω/β vitesse de phase.
Le temps de propagation de groupe est définit par :
Tg = dβ/dω

3. Cas particulier des lignes sans pertes.
Dans ce cas, R=G=0 (il n'y a pas d'affaiblissement).
Zc = sqrt(L/C)
γ² = -LCω²
Β = ω.sqrt(LC)
En x=0 on en déduit Vo = V1 + V2 et Io = (V1 - V2)/Zc Soit V1=(V0+ZcIo)/2 et V2=(V0-ZcIo)/2
v(x) = V1exp(-γx) + V2exp(γx) = V0.ch(γx) -Zc.Io.sh(γx)
i(x) = (-Vo/Zc).sh(γx) + Io.ch(γx)
Z(x) = Zc.[Zo-Zc.th(γx)]/[Zc-Zo.th(γx)]
z(x) = Z(x)/Zc = impédance réduite.
V(x) = Vr.cos(βx)+j.Zc.Ir.sin(βx)
I(x) = Ir.cos(βx)+j.(Vr/Zc).sin(βx)
z(x) = [zr+j.tg(βx)]/[1+j.zr.tg(βx)] = impédance réduite.
ch(γx) devient cos(βx)
sh(γx) devient j.sin(βx)
th(γx) devient j.tan(βx)
Calcul du coefficient de réflexion &ro; et du ROS :
&ro; = V-/V+ = (V2/V1).exp(2.j.γ.x) = [(zo-1)/(zo+1)].exp(2.j.γ.x)
ROS = (1+|&ro;|)/(1-|&ro;|)

4. Cas particulier de charge.
Dans le cas ou la ligne est en court circuit, Zr=0 et Vr=0.
V(x) = j.Zc.Ir.sin(βx)
I(x) = Ir.cos(βx)
z(x) = j.Zc.tg(βx)
Z(x) = Zc/[j.tg(βx)]
Dans le cas de la ligne quart d'onde, l=λ/4Z(x) = [zr+j.tg(β.λ/4)]/[1+j.zr.tg(β.λ/4)] = 1/zr
C'est un inverseur d'impédance, si zr est capacitif, λ/4 avant on est inductif ; de même si zr est inductif, λ/4 avant on est capacitif.
Partant de là, ne nous arrétons pas en si bon chemin :
Les paramètres S et l'abaque de Smith.