Encodeur Reed-Solomon paramétrable.
Introduction.
Les codes Reed Solomon appartiennent à la classe des codes non binaires, les symboles ne sont donc plus des éléments qui valent '0' ou '1' mais sont des éléments d'un corps fini. www.opencores.org propose les sources d'un codeur RS, au format Verilog peu clair et sans explications suffisantes. Quelques autres sources diffusent des informations parfois pertinentes, souvent erronées mais en tout état de cause, jamais exhaustives, à défaut trop sommaires. Remédions à cet état de fait et expliquons en "succinctement" le principe dans l'optique d'une synthèse matérielle type FPGA. Les quelques pré-requis indispensables sont ici : terminologie des codes correcteurs.Polynôme générateur et polynôme primitif.
L'arithmétique des champs finis fut découverte par Evarsite Galois (1811 Bourg-la Reine, 1832). Un corps de Galois est un ensemble pour lequel le résultat de certaines opérations arithmétiques (addition, multiplication...) entre deux éléments du corps est un autre élément du corps. Un polynôme primitif p(x) est utilisé pour définir les éléments du corps de Galois GF ; à chaque largeur de symbole correspond quelques polynômes primitifs valident de degré n pour un symbole de n bits. Dans le cas d'un traitement au niveau octet le polynôme le plus généralement utilisé est :p(x) = 1 + x2 + x3 + x4 + x8 = 1 0 1 1 1 0 0 0 1 = 285 Largeur du symbole et polynômes primitifs valident.
| Symbol Width | Valid field polynomials (decimal representation) |
|---|---|
| 3 | 11,13 |
| 4 | 19,25 |
| 5 | 37,41,47,55,59,61 |
| 6 | 67,91,97,103,109,115 |
| 7 | 131,137,143,145,157,167,171,185,191,193,203,211,229,241,247,253 |
| 8 | 285,299,301,333,351,355,357,361,369,391,397,425,451,463,487,501 |
g(x) = (x + Alpha^0).(x + Alpha^1). ... .(x + Alpha^15)Dans l'arithmétique des corps de Galois, addition et soustraction sont exactement identiques; cette expression de g(x) peut donc être représentée de façon similaire avec des signes moins au lieu des signes plus. Soit dans un cas plus général :
g(x) = Produit de i=b à b+n-k-1 [(x - Alpha^i)]Notons que 'b' peut prendre n'importe quelle valeur entière, il est toutefois beaucoup plus simple de choisir la valeur zéro. Cependant le choix de cette valeur est dicté par les normes ; si b=0 pour les utilisations DVB et CWDM, b vaudra 120 pour le cas AAL-1 de l'ATM. Le choix de cette valeur influencera les coefficients du polynôme générateur mais aussi certaines caractéristiques du décodeur ; les racines de g(x) permettant le calcul des coefficients du syndrome. Ces définitions étant énoncées, regardons le fonctionnement de l'arithmétique dans un corps fini de Galois.
Coefficients du polynôme générateur.
Pour calculer les symboles de redondance, il faut connaître les coefficients du polynôme générateur. Intéressons nous au code RS(7,3,5) dans GF(2^3^) ou p(x) = x^3^ + x + 1 est polynome primitif, donc p(Alpha) = Alpha^3^ + Alpha + 1 = 0 et avec :g(x) = produit de i=0 à n-k-1 (x + Alpha^i) g(x) = (x + 1).(x + Alpha^1).(x + Alpha^2).(x + Alpha^3)Le développement de g(x) donne après suppression des puissances de alpha identiques :
x^4^ : 1
x^3^ : Alpha^3^ + Alpha^2^ + Alpha + 1
x^2^ : Alpha^5^ + Alpha^4^ + Alpha^2^ + Alpha
x^1^ : Alpha^6^ + Alpha^5^ + Alpha^4^ + Alpha^3^
x^0^ : Alpha^6^
Soit après addition des notations binaires associées :
g(x) = x^4 + Alpha^2.x^3 + Alpha^5.x^2 + Alpha^5.x + Alpha^6Regardons maintenant le cas du code RS(15,9,7) dans GF(2^4^) dont un polynôme primitif est p(x) = x^4^ + x^3^ + 1 donc p(Alpha) = Alpha^4^ + Alpha^3^ + 1 = 0 et g(x) = Produit de i=1 à 6 de (x + Alpha^i^) avec ici b=1.
g(x) = x^6 + Alpha^12.x^5 + x^4 + Alpha^2.x^3 + Alpha^7.x^2 + Alpha^11.x + Alpha^6Il est facile de vérifier le terme en x^0^ qui vaut le produit des Alpha soit Alpha^6.Alpha^5.Alpha^4.Alpha^3.Alpha^2.Alpha = Alpha^(6+5+4+3+2+1)mod(15) = Alpha^6 Le calcul manuel des autres coefficients est fastidieux, il vaut mieux utiliser un algorithme en C par exemple. Tentons d'expliquer comment fonctionne cet algorithm qui sera plus tard le coeur de l'encodeur. Rappelons tout d'abords le triangle de Pascal qui permet de calculer les coefficients du développement de (x+1)^n
(x+1)^0 | 1
(x+1)^1 | 1 1
(x+1)^2 | 1 2 1
(x+1)^3 | 1 3 3 1
(x+1)^4 | 1 4 6 4 1
for (ligne = 1; ligne <= red; ligne++) {
tab_coef[ligne] = 1;
for (colonne = ligne-1; colonne > 0; colonne--)
tab_coef[colonne] = tab_coef[colonne-1] + tab_coef[colonne];
fin pour;
fin pour;
Le calcul des coefficients du polynôme générateur est largement inspiré de cet algorithme mais utilise en plus certaines notions mathématiques de la théorie des corps, à savoir l'addition et la multiplication. Petit rappel pour les moins courageux ; la multiplication est réalisée en additionnant modulo 2^m^ les puissances de alpha, l'addition est le ou exclusif des formes vectorielles. Regardons le développement jusqu'à l'ordre 3 du produit des (x + Alpha^i^)
0 | 1
1 | 1=a : 0+1.Alpha^0^=b
2 | 1=c : b+a.Alpha^1^=d | 0+b.Alpha^1^=e
3 | 1=f : d+c.Alpha^2^=g | e+d.Alpha^2^=h | 0+e.Alpha^2^=i
tab_coef[w] = Alpha^(ligne-1).tab_coef[w-1] + tab_coef[w];
// colonne(i) = colonne(i-1).A^(ligne-1) xor colonne(i)
// Note1 : index_of(vector) retourne la puissance de alpha.
// exemple : index_of(6) retourne 4
// Note2 : pour effectuer la multiplication prendre la puissance de alpha
// de colonne(i-1) puis appliquer la relation :
// alpha^i.alpha^j = alpha(i+j)modulo(2^m)
// Note3 : pour effectuer le xor : prendre index_of(valeur) afin de calculer
// sur les valeurs décimales.
// Le résultat obtenu sera sous forme décimale. (vector)
// Nous trouvons par calcul et pour une valeur initiale b=0 puis b=1 :
gin(0) = 59 pour b=0, 79 pour b=1
gin(1) = 36 pour b=0, 44 pour b=1
gin(2) = 50 pour b=0, 81 pour b=1
gin(3) = 98 pour b=0, 100 pour b=1
gin(4) = 229 pour b=0, 49 pour b=1
gin(5) = 41 pour b=0, 183 pour b=1
gin(6) = 65 pour b=0, 56 pour b=1
gin(7) = 163 pour b=0, 17 pour b=1
gin(8) = 8 pour b=0, 232 pour b=1
gin(9) = 30 pour b=0, 187 pour b=1
gin(10) = 209 pour b=0, 126 pour b=1
gin(11) = 68 pour b=0, 104 pour b=1
gin(12) = 189 pour b=0, 31 pour b=1
gin(13) = 104 pour b=0, 103 pour b=1
gin(14) = 13 pour b=0, 52 pour b=1
gin(15) = 59 pour b=0, 118 pour b=1
tab_coeff(0) := alpha_to(init_zero); -- forme vectorielle de alpha^init_zero
tab_coeff(1) := 1; -- ligne 1 : init : g(x)=(X+alpha^init_zero)
for ligne in 2 to nn-kk loop -- 2 to nn-kk
tab_coeff(ligne) := 1; -- poids fort forcément à 1
for colonne in ligne-1 downto 1 loop
interne1 := (index_of(tab_coeff(colonne))+ligne-1+init_zero) mod (f_xy(mmm)-1);
tab_coeff(colonne) := to_integer(
to_unsigned( alpha_to(interne1),mmm ) xor
to_unsigned( tab_coeff(colonne-1),mmm )
);
end loop;
tab_coeff(0):=alpha_to((index_of(tab_coeff(0))+ligne-1+init_zero)mod(f_xy(mmm)-1));
end loop;
Encodeur Reed-Solomon : principe.
Le code RS utilisé pour la TNT ou tout autre système DVB permet de corriger 8 octets erronés par paquet de transport. Ce mécanisme ajoute donc 16 octets de redondance au message d'information afin d'obtenir un mot de code (204,188,8) : (n,k,t). Ce mécanisme pouvant corriger jusqu'à 8 symboles est un code adapté pour corriger les erreurs en rafale (burst) introduites par le canal de transmission (voies hertziennes terrestres). Le code (204,188,8) est une version raccourcie de (255,239,8) qu'il est possible d'utiliser en ajoutant 51 octets nuls avant les 188 d'information. En sortie de codeur, les octets nuls sont supprimés le code bloc étant ainsi ramené aux 204 symboles utiles. Cette dernière méthode semble toutefois peu élégante et délicate à mettre en oeuvre : une solution plus souple sera utilisé. Revenons à l'encodage Reed-Solomon ; le polynôme g(x) est de la forme :g(x) = (x - α^(b)) + (x - α^(b+1)) + ... + (x - α^(b+2t-1)) c(x) = i(x) + rem(x) = i(x) . x^((n-k)) + [i(x) . x^((n-k))]. mod g(x)Le principe est exactement le même que pour un encodeur binaire CRC, la grande différence étant que les valeurs à manipuler sont des symboles qui nécessitent l'utilisation d'additions et multiplications dans CG. La partie à gauche du signe + de l'équation signifie que l'on décale les symboles d'information vers les puissances de x les plus élevées de n-1 à n-k ; ces k premiers coefficients sont donc les symboles d'information d'origine, les n-k valeurs qui suivent constituent les symboles de redondance : le code est systématique. L'architecture d'un encodeur est représentée par le schéma suivant.
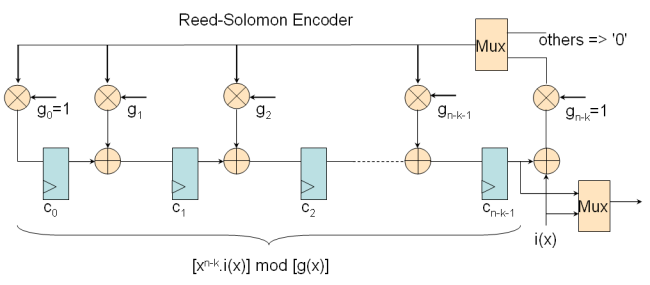
Encodeur Reed-Solomon : description VHDL.
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
use work.pkg_rs.all;
entity rs_encoder is
generic(nn : integer:=128; -- nombre total de symbole par bloc
kk : integer:=124); -- nombre de symbole d'information par bloc
port(xgsr : in std_logic; -- reset global asynchrone
clk : in std_logic; -- horloge de traitement
ce : in std_logic; -- clock enable
din : in symbole; -- Bus de donnée d'entrée
start : in std_logic; -- A '1' au premier octet de calcul FEC
ce_fec : in std_logic; -- A '1' lors du calcul du fec
dout : out symbole); -- mot de code de sortie
end rs_encoder;
architecture A of rs_encoder is
-- gin_0.....gin_i (8 bits each ) = Generator polynomial co-effcients.
-- The generator polynomial is form
-- X^(i+1) + gin_i X^i + gin_i-1 X^(i-1) + ...... gin1 X + gin0.
-- Each gin_i (i=0, 1, ..., nn-kk) is an element of GF(2^8).
--
-- b+n-k-1
-- ____
-- g(x) = | | (x + alpha^i)
-- | |
-- i=b
--
-- Calcul des coefficients du polynome générateur pour le cas de l'ATM :
-- G(x)=(x-a^120)(x-a^121).(x-a^122).(x-a^123)
-- G(x)=(x^2 + x.a^145 + a^241).(x^2 + x.a^147 + a^245)
-- G(x)=(x^4 + x^3.a^195 + x^2.a^234 + x.a^183 + a^245)
signal gin : tab_symbole(nn-kk-1 downto 0);
signal fback : std_logic_vector(mm-1 downto 0);
signal val_fec : tab_symbole(nn-kk-1 downto 0);
begin
gin <= f_cal_gin(mm,nn,kk,init_zero, poly_prim);
fback <= (val_fec(nn-kk) xor din) when (ce_fec='1') else (others => '0');
cal_rs_proc: process(xgsr,clk)
begin
if (xgsr ='1') then
for i in 0 to nn-kk-1 loop
val_fec(i) <= (others =>'0');
end loop;
dout <= (others =>'0');
elsif rising_edge(clk) then
if (ce='1') then
-- val_fec = x^(n-k).u(x).mod[g(x)]
val_fec(0) <= f_gfmult8(fback, gin(0));
for i in 1 to nn-kk-1 loop
val_fec(i) <= val_fec(i-1) xor f_gfmult8(fback, gin(i));
end loop;
-- mux output control : k information symbol and n-k parity
if (ce_fec='1') then
dout <= din;
else
dout <= val_fec(nn-kk-1);
end if;
end if;
end if;
end process cal_rs_proc;
end A;
Analyse de l'encodeur Reed-Solomon.
Le code est relativement concis et paramétrable, le package comprend une fonction qui permet le calcul des coefficients du polynome générateur ainsi que les équations de la multiplication. Les heureux propriétaires de Core-generator, outil xilinx, pourront corréler les résultats fournis par le core avec ceux du code proposé, les autres se contenteront d'un calcul de syndrome. Vérifier la fonction de multiplication dans le corps est chose facile : il suffit de comparer la formule mathématique (somme des puissances de alpha modulo 255) avec le calcul de la fonction VHDL. Pour les coefficients le core xilinx confirme les valeurs : pour cela nous utiliserons un pattern spécifique ou toute la charge est nulle sauf le dernier symbole à 01, soit i(x)=1 : dans ce cas, et sans insertion d'erreur, les symboles de redondance correspondent aux coefficients du polynome générateur ; avec ce pattern, la fonction de multiplication n'est pas utilisée, nous vérifions donc simplement l'ordre des symboles et les coefficients 'gi'. Pour d'autres messages d'information, cela se complique, il faut corréler avec une source dont nous sommes sur.Il était une fois ... Les codes correcteurs d'erreurs.
- Terminologie des codes correcteurs.
- Les codes de redondance cyclique.
- Corps finis : principes.
- Décodeur Reed-Solomon : syndrome et incertitude.
- LFSR tool CRC/syndrome/Galois multiplier.
Littérature, notations & documentation.
The art of error coding,Robert Morelos-Zaragoza,
Wiley Pierre Csillag
Introduction aux Codes Correcteurs
Ellipses, Paris, 1990 Sources VHDL de l'encodeur Reed Solomon.
package de l'encodeur Reed Solomon.
Code source en C de cacul des coefficients du polynome générateur
Compiler un code source avec gcc :
cc new2_rs_erasures.c -DNO_PRINT -lm -o rsgp
cc rs_cal.c -o rs_cal Source d'informations sur les codes correcteurs, Programmes en C.
Introduction aux CCE.
part 1 : Viterbi codecs.
part 2 : Reed-Solomon codecs.
Reed-Solomon Codec Design in Programmable Logic.
Projet encodeur RS de opencores.
Codes linéaires, codes cycliques, corps de Galois.
Multiplieur dans le corps de Galois.
Librairie scientifique et technique Lavoisier.
CRC : Code de Redondance Cyclique. RS : Reed Solomon. ECC/CCE : Code Correcteur d'erreurs. FEC : Forward Error Coding. GF(n) : Galois Fields, champs de Galois. LFSR : Linear feedback shift register. n : n symbols from block eencoding (longeur totale avec parité). k : k symbols information (uer payload). t : Error correcting capability = (dmin-1)/2 dmin : minimum Hamming distance. C(n,k,dmin) rem(x) : polynôme de redondance d'ordre n-k.