Corps de Galois, symboles, codes en bloc, poids de Hamming, distance de Hamming, polynôme générateur, polynôme primitif, matrice génératrice, matrice de parité, syndrome, effacement. Les codes correcteurs d'erreurs (CCE) sont de plus en plus utilisés dans les technologies de transmission de l'information ou dans l'aérospatiale. Les CCE peuvent être divisés en deux grandes familles : codes en blocs et codes récurrents. Dans la deuxième famille, qui sont des codes séquentiels ou convolutif, un effet de mémoire est introduit (exemple : codage Viterbi), cela sera l'objet d'un autre article. Le terme FEC (Forward Error Correction) détermine une correction d'’erreur directe alors que le terme ARQ (Automatic Repeat Request) correspondra à une demande automatique de répétition.
Terminologie et définitions.
On appelle code en bloc (ou block code) un code ou les symboles issues de la source d'information sont regroupés par blocs de k. Dans le cas de la TnT et plus généralement DVB, k est un bloc de 188 octets issue du transport stream MPEG, dans les télécommunication CWDM (trame OTN G709) k sera une décomposition d'une ligne de la trame et vaudra 239 octets. 'n' correspondra à la taille du bloc après codage, n sera supérieur à k afin de satisfaire la condition de redondance. n-k correspondra donc au nombre de symbole de parité ajouté par le codeur et vaudra 16 pour les deux exemples cités plus haut. Le code est dit systématique si les k premiers symboles du bloc encodé sont égaux aux symboles du bloc d'information. Le rendement d'un code C(n,k) vaut R = k/n.
Les symboles appartiennent à un alphabet de q éléments, ils seront dits q-aires : binaire, quartet, octet ; GF(q) désigne le corps de Galois, par exemple GF(2) possède deux éléments {0,1} ces éléments sont utilisés pour les codes binaires type CRC, Hamming, Reed Muller...
Un corps étendu de Galois sera noté GF(p^m) : corps fini pour lequel q=p^m et ou le nombre de symbole est un entier puissance du nombre premier p. Par la suite p vaudra 2 et dans le cas le plus usité, m vaudra 8 : les mécanismes fonctionneront sur des symboles de type octet. Cette extension du corps de Galois est utilisé dans la famille des codes non binaires type Reed-Solomon.
Petit exemple.
Imaginons que l'on veuille appliquer un code détecteur d'erreurs sur la valeur de l'année civile, le mot d'information est composé de quatre chiffres, nous ajouterons un cinquième chiffre de redondance somme modulo 10 des quatre chiffres d'information : 20057, 20068. Ce code est linéaire , la somme de deux codes donnant un code valide : 40015 ; le code est systématique par contre le code n'est pas cyclique 72005 n'étant pas un code valide.Métrique de Hamming.
Le poids de Hamming, wmin, d'un mot est le nombre de bits à 1 qu'il contient. La distance de Hamming entre deux mots de même longueur est définie par le nombre de positions binaires qui diffèrent entre ces deux mots : le nombre de 1 dans le XOR résultant. La distance de Hamming d'un code, notée dmin, est la distance minimum entre tous les mots du code. Si C(n,k) est un code bloc linéaire, la somme de deux mots du code est aussi un mot du code, il en résulte que dmin = wmin. Le calcul de d_min nécessiterait 2^k(2^k-1) ce qui serait long à calculer même pour un code de taille modeste. Pour un code linéaire, le calcul de d_min nécessite de calculer "seulement" le poids de hamming des 2^k^-1 mots de code non nuls. Si d_min est la distance minimale de hamming d'un code, il est possible de montrer que le nombre maximum d'erreurs détectable est (dmin - 1) alors que le nombre d'erreurs corrigibles est t = (dmin - 1)/2. Certains canaux sont dit à effacement ; dans ce cas le récepteur peut déclarer le symbole reçu incertain, soit parce que le symbole est trop loin du seuil de décision (modulation QAM) soit à la suite d'une perte de donnée dans une structure à entrelacement (ATM-AAL-1). Le décodeur peut alors corriger jusqu'à (dmin - 1) effacement. Un code sera donc caractérisé par trois paramètres n, k, dmin et noté C(n,k,dmin) nous trouverons parfois la notation C(n,k,t) ou C(n,k,2t) avec t représentant le nombre d'erreur corrigible.Structure général d'un encodeur.
Un encodeur est régit par les polynômes suivants :p(x) = x^8 + x^4 + x^3 + x^2 + 1 g(x) = Produit de i=b à b+n-k-1 de (x - Alpha^i)qui sont le polynome primitif et le polynôme générateur. Le polynôme primitif est utilisé uniquement dans le cas de codes non binaires tel que les codes Reed-Solomon. Les 'k' symboles d'information constituent un polynôme i(x) d'ordre k-1. L'information de redondance r(x) est d'ordre n-k-1 et correspond au reste de la division euclidienne du polynôme d'information par le polynôme générateur g(x).
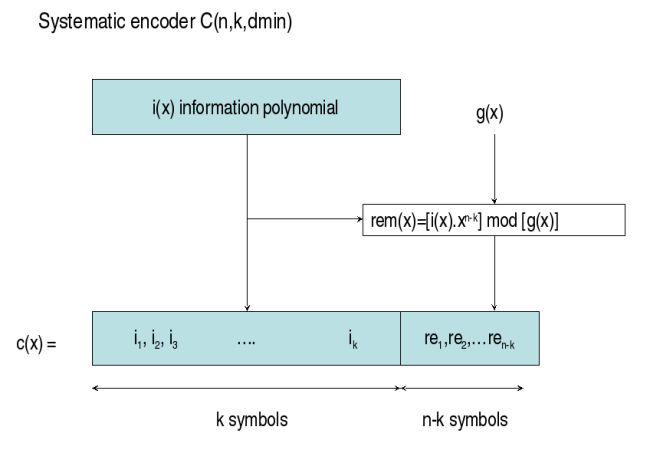
Transmission de l'information.
Le canal de transmission introduit par la suite une erreur notée e(x) sous sa forme polynomiale; le décodeur recevra donc r(x) = c(x) + e(x). Si la transmission est sans erreur, e(x)=0 et r(x)=c(x).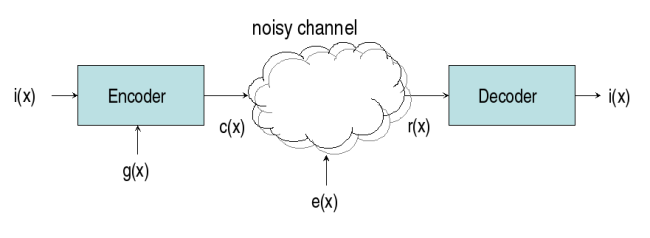
i(x) polynôme d'information de degré k-1 g(x) polynôme générateur d'ordre n-k c(x) polynôme mot de code de degré n-1 e(x) polynôme d'erreur de degré n-1 r(x) polynôme reçu de degré n-1 s(x) polynôme syndrome de degré n-k-1Une transmission sans erreur signifie que le bloc de code reçu r(x) est multiple de g(x), il faut calculer le syndrome, reste de la division de r(x) par g(x). Dans le cas des codes non binaires, les coefficients de s(x) correspondent à l'évaluation du mot reçu pour les différentes racines de g(x).
Matrice génératrice, matrice de parité et calcul de d_min
Considérons un code linéaire dont le polynôme générateur est g(x)=x^3^ + x + 1 et noté C(7,4,3). Le code est linéaire et systématique il peut donc être représenté par sa matrice génératrice G = [I|P] ou I représente la matrice identité (le mot d'information est conservé) et P la matrice parité. c(x) = i(x).G
G = (1000|101) x^n-1 mod g(x) = x^6 mod (x^3 + x + 1) = x^2 + 1
(0100|111) x^n-2 mod g(x) = x^5 mod (x^3 + x + 1) = x^2 + x + 1
(0010|110) x^n-3 mod g(x) = x^4 mod (x^3 + x + 1) = x^2 + x
(0001|011) x^n-k mod g(x) = x^3 mod (x^3 + x + 1) = x + 1
Le polynôme de parité est donné par h(x) = x^n^+1/g(x) = h0 + h1.x + ... + hk.x^k^ soit h(x)=1+x+x^2^+x^4^ dans notre exemple. Nous pouvons alors définir la matrice parité H=[I|Pt] avec Pt transposée de la matrice P. Pour rappel, la transposée d'une matrice A n.m est notée At de dimension m.n obtenue en échangeant les lignes et les colonnes.
Il était une fois ... Les codes correcteurs d'erreurs.
- Les codes de redondance cyclique.
- Encodeur Reed-Solomon.
- Corps finis : principes.
- LFSR tool CRC/syndrome/Galois multiplier.
Liens externes.
Wikipedia : code correcteur.ECC page.
Glossaire.
FEC Forward Error Correction / correction d’erreur directe ARQ Automatic Repeat Request / demande automatique de répétition CRC Cyclic Redundancy Check ECC Error Checking Code C(n,k) Code de longueur totale n k Longeur d'information utilisateur (source) n-k longueur de la parité (redondance) g(x) generator polynomial h(x) Parity check polynomial i(x) information polynomial c(x) transmit code polynomial r(x) receive code polynomial e(x) error polynomial s(x) syndrome polynomial