Un Code de Redondance Cyclique (CRC) est un code correcteur d'erreur (CCE) sous-classe des codes blocs linéaires : introduction & terminologie des CCE. Les codes CRC sont très utilisés dans les systèmes de communications pour le contrôle et la détection d'erreur ; la première étude des codes cycliques fut faite par Eugène Prange en 1957. Un code CRC est linéaire, systématique et bien sur cyclique ; comme vous avez lu l'introduction, ces termes vous sont donc familiers et nous pouvons passer aux choses sérieuses.

Codes utilisés et applications.

Description Polynome n-k (redondance)
CRC-7 TTI trace J1 x^7^+x^3^+1 7 bits
CRC-8 ATM HEC x^8^+x^2^+x+1 8 bits
CRC-10 ATM-OAM x^10^+x^9^+x^5^+x^4^+x+1 10 bits
CRC-16 ATM QoS/RFID x^16^+x^12^+x^5^+1 16 bits
CRC-16 CCITT x^16^+x^15^+x^2^+1 16 bits
CRC-16 GFP-T CRC-16-GFPT 16 bits
CRC-32 Ethernet CRC-32-Eth 32 bits

CRC-16-GFPT
g(x) = x16 + x15 + x12 + x10 + x4 + x3 + x2 + x + 1
CRC-32-Eth
g(x) = x32 + x26 + x23 + x22 + x16 + x12 + x11 + x10 + x8 + x7 + x5 + x4 + x2 + x + 1

Un peu de mathématiques.

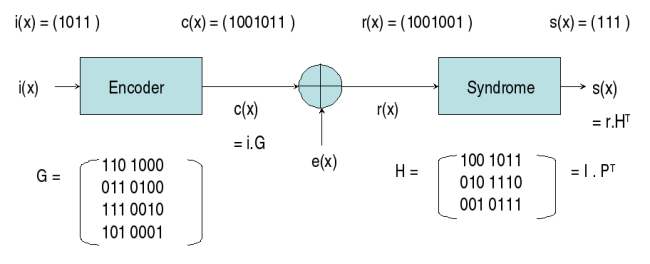
Soit un code C(n,k) ou 'n' est la longueur totale du code après ajout de la parité, et 'k' est la longueur du champ d'information. 'n-k' représente la longueur du champ de redondance ainsi que le degré du polynôme générateur g(x). Le flux de données d'information sur lequel est calculé le CRC est décomposé en bloc de longueur 'k' constituant un polynôme i(x); le CRC correspond au reste de la division binaire modulo 2 de i(x) sur g(x). Afin de rendre le code systématique, le reste est ajouté a la suite du message d'information ; cela permet d'obtenir un code bloc multiple du polynôme générateur.

Considérons deux polynômes i(x) et g(x), il existe un unique couple q(x) et rem(x) qui vérifie [eqtn1] qui sont le quotient et le reste. 
i(x) = q(x)g(x) + rem(x) [eqtn1]
c(x) = i(x) + rem(x) = q(x)g(x) [eqtn2]
r(x) = c(x) + e(x)
s(x) = r(x)/g(x) = e(x)/g(x)
Coté réception nous vérifions que le code reçu r(x) est bien multiple de g(x), le bloc reçu, donc crc compris, est divisé par le polynôme générateur g(x) ; le reste est nul si la transmission est effectuée sans erreur. Sinon le résultat obtenu, appelé valeur de syndrome, est fonction de la position de l'erreur. Remarquons qu'il est nécessaire de calculer le syndrome afin de pouvoir corriger d'éventuelles erreurs ; il est possible de simplement calculer un nouveau CRC pour uniquement savoir si le bloc reçu est erroné ou non. Si le vecteur d'erreur e(x) est non nul et multiple de g(x) alors le détecteur analysera la séquence reçue comme étant multiple du polynôme générateur, la somme de deux mots de code valident étant un mot de code valide. Il en résulte que tout pattern d'erreurs multiple de g(x) ne peut être détecté.

Encoder un code cyclique.

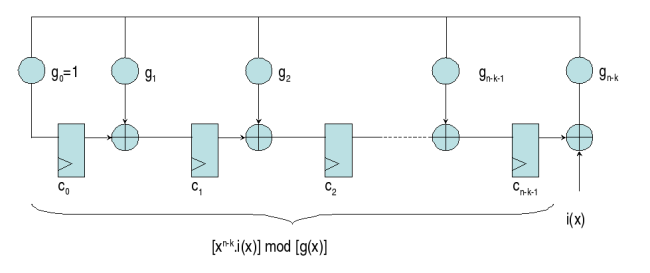
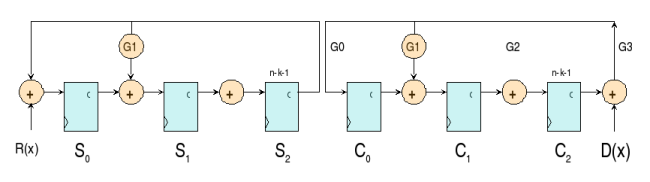
Considérons un code cyclique C(n,k) = C(7,4) composé de 4 bits d'information et 3 bits de redondance utilisant pour polynôme générateur g(x)=1 + x + x^3. L'implémentation d'un codeur série utilise une LFSR qui permet de multiplier i(x) le polynôme d'information par X^(n-k) et de diviser ensuite par g(x). L'encodage est dit systématique : les k premières valeurs constituent le message, les n-k suivantes la redondance qui rend le code multiple de g(x). Le code est binaire et utilise le corps CG(2)={0,1} auquel appartiennent les coefficients gi du polynôme générateur.

Approche mathématique :
Une première méthode consiste à calculer le mot de code c(x) à partir de la matrice génératrice ; G n’étant généralement pas sous une forme systématique, il est nécessaire de réaliser quelques opérations qui donnent G’: La matrice génératrice est de dimension ‘n.k’ soit dans l’exemple (7,4).
c(x) = i(x).G' = {1001}.G' = 1.g0 + 0.g1 + 0.g2 + 1.g3 = 011 1001
c(x) = i(x).G' = {0010}.G' = 0.g0 + 0.g1 + 1.g2 + 0.g3 = 111 0010

Une deuxième méthode utilise la division binaire polynomiale (modulo 2). 
 x^5           /  x^3 + x + 1 = g(x)       i(x) = x^2 = {0100}
 x^3 + x^2        x^2 + 1 = q(x)           r(x) = x^2+x+1 = {111} 
 x^2 + x + 1                               c(x) = 111.0010
 r(x) = crc = {111}

 x^6 + x^3     /  x^3 + x + 1 = g(x)       i(x) = 1+x^3 = {1001}
 x^4              x^3 + x = q(x)           r(x) = x^2+x = {110} 
 x^2 + x                                   c(x) = 011.1001
 r(x) = crc = {110}

Détection et correction d'erreurs.

Afin de pourvoir corriger les erreurs éventuellement introduites par le canal de transmission, il est nécessaire de calculer le syndrome. Le code reçu est cette fois divisé par g(x) ; une fois les 'n' bits reçus la LFSR contient la valeur du syndrome qui est nulle en absence d'erreur, sinon la valeur est uniquement fonction de l'erreur e(x) : à chaque valeur de syndrome correspond un vecteur d'erreur unique. Un décodeur simple pourra donc tabuler la table syndrome/erreur.

Vecteur d'erreur et syndrome associé.
e(x) bin. e(x) s(x)
0000001 x^6^ 101 (101)
0000010 x^5^ 111 (111)
0000100 x^4^ 011 (110)
0001000 x^3^ 110 (011)
0010000 x^2^ 001 (100)
0100000 x^1^ 010 (010)
1000000 x^0^ 100 (001)

Les valeurs de syndromes qui correspondent à une erreur corrigible correspondent aux 'n' premiers coefficients du corps de Galois GF(2n-k) que l'on construirait en utilisant g(x) comme polynôme primitif. Il est donc possible de calculer les valeurs attendus de syndromes qui sont des constantes élaborées lors de la compilation du projet.

Calcul des syndromes attendus.

Cette fonction permet donc de définir la table des valeurs de syndromes associée aux vecteurs d'erreur. La valeur init correspond au reste de e1(x)/g(x) ou e1(x) représente le premier vecteur d'erreur qui vaut généralement 1 et donc init=x"0001" ; en GFP-T le code C(536,520) permet en plus de corriger les erreurs doubles espacées de 43 bits, dans ce cas e1(x)=1+x^43 (c'est le polynôme de l'embrouilleur), et donc init=x"4DA3". Bien sur la table des erreurs doubles contient n-43 valeurs, les dernières étant simples à l'intérieur du bloc, la duplication se retrouvant sur le bloc suivant. Petit exemple :
Le mot d'information i(x)={1011} associé à la redondance {100} donne c(x)={100 1011} considérons e(x)={0010000} erreur introduite à la position x2. Le mot reçu est alors r(x)={101 1011} et le syndrome calculé s(x)={001} ce qui permet de conclure selon la table ci-dessus une erreur en position x2 et donc de retrouver le mot d'émission c(x)=e(x)+r(x)=0010000 + 1011011 = 1001011. La table ainsi que la complexité de recherche croit exponentiellement avec la longueur du code et le nombre d'erreurs corrigibles ; une méthode plus optimisée doit donc être employée pour les codes de longueur importante.

Correction des erreurs avec un décodeur cyclique série.

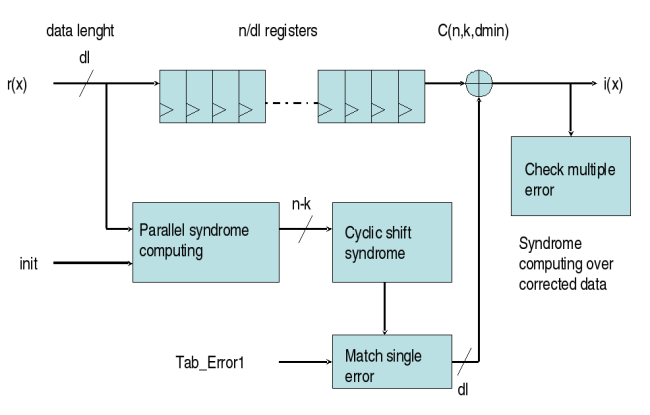
Une des propriétés des codes cycliques permet de s'affranchir de la table d'erreur et d'optimiser le code permettant la correction d'erreur. Après calcul, le syndrome sert d'initialisation à la LFSR qui permutera le résultat n fois. Considérons une erreur en position xi . Le code étant cyclique, après n-i cycles les registres de la LFSR contiendront la valeur de syndrome associé à l'erreur de plus haut degré. Reprenons l'exemple précédent avec e(x)=x2 ; le syndrome associé à l'erreur de plus haut degré est 101. Pour une message transmis c(x)= 100.1011 nous recevrons r(x)=101.1011 et le syndrome calculé sera 001 (S0S1S2). Quatre cycles après le registre de la LFSR contiendra la valeur 101 puis le cycle suivant 000 du fait que le code est complet : à une valeur de syndrome correspond un pattern d'erreur simple, ce qui n'est pas toujours le cas. L'inconvénient majeur de cette méthode réside dans le fait que la recherche est effectuée cycliquement pour chaque position d'erreur possible; la latence du mécanisme est donc de 'n', le nombre de bit dans le bloc. Par contre le coeur de traitement n'utilise qu'une LFSR.

Décodeur cyclique en mode parallèle.

Cette solution combine les deux méthodes précédentes ; un traitement série cyclique pouvant être trop long, et un décodage brut des coefficients de syndrome trop lourd. LA solution consiste donc à faire tourner cycliquement le syndrome en mode parallèle. Par exemple, pour corriger l'en-tête ATM de 5 octets dont un de redondance, la table des vecteurs d'erreur est la suivante :
80 x32 89 x24 B6 x16 0B x8 31 x0
40 x33 C7 x25 5B x17 86 x9 9B x1
20 x34 E0 x26 AE x18 43 x10 CE x2
10 x35 70 x27 57 x19 A2 x11 67 x3
08 x36 38 x28 A8 x20 51 x12 B0 x4
04 x37 1C x29 54 x21 AB x13 58 x5
02 x38 0E x30 2A x22 D6 x14 2C x6
01 x39 07 x31 15 x23 6B x15 16 x7

Un vecteur d'erreur x39 générera une valeur de syndrome 01 qui sera cycliquement permutée dans le calcul parallèle du syndrome. Après 4 cycles la valeur du syndrome sera 16, ce qui correspond à une erreur en position x7 ; nous comprenons alors aisément qu'il est possible de décoder uniquement la dernière colonne de syndrome ce qui donne la structure suivante de décodeur :

Décodeur cyclique parallèle.

Performance d'un CRC et interaction avec un embrouilleur.

Afin de permettre au récepteur d'effectuer une récupération d'horloge, il est indispensable de ne pas avoir de longues suites de '0' ou de '1'. La raison de l'embrouilleur de type auto synchronisé est en fait tout autre : "Frames are scrambled to protect a user from other malicious users who may try to cause loss of receiver synchronization at the physical layer." Les données sont donc embrouillées par le biais d'un polynome scr(x)=x43 + 1. En présence d'erreurs de transmissions, le désembrouilleur les propagera. Lors du calcul du syndrome, c(x) étant multiple de g(x) le reste de c(x)/g(x) sera nul, il en sera de même pour le reste du produit c(x)scr(x)/g(x). Les erreurs seront donc propagées par le terme e(x)scr(x). 
[c(x) + e(x)].scr(x) = c(x)scr(x) + e(x)scr(x)
f(x) = e(x)scr(x)
Si scr(x) est multiple de g(x) la fonction d'erreur f(x) aura g(x) comme facteur et générera un reste nul supprimant ainsi la pouvoir correcteur du code CRC. Dans le cas GFP-T, le choix du polynôme CRC-16 fut réalisé afin de ne pas avoir de facteur commun entre scr(x) et g(x) ce qui n'est pas le cas pour le CRC-10 de l'ATM. Une erreur simple est propagée par le désembrouilleur 43 bits plus loin, comme l'embrouilleur n'est pas réinitialisé à chaque code bloc CRC, l'erreur dupliquée peut se produire sur le code suivant.

Interaction entre CRC et embrouilleur.

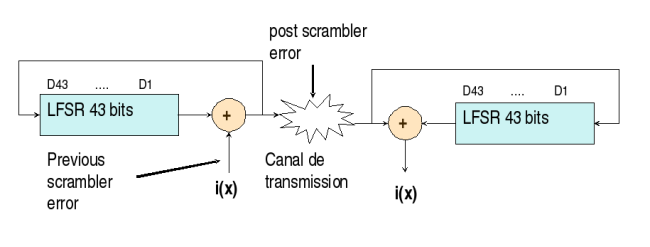"Self synchonous scrambler uses x^43^+1 polynomial (GFP, ATM...). This means each payload bit is eXclusive OR (XOR) with scrambler output which is payload bit previous 43 cycle. Superblock from GFP-T are scrambled , so each transmission error results in a pair of errors in the descrambled data : CRC '''must''' cope with this error multiplication. The subject of error multiplication was well covered by numerous mathematicians for the PPP-over-SONET standard. In the end, they chose a self-synchronizing x^43^+1 scrambler with 2-bit error multiplication for anti-jamming purposes. It is possible to prove that a given self-synchronizing scrambler does not reduce the CRC power. To avoid interaction between different CRC (Ethernet for exemple), the sole requirement is that the scrambler must have no common factors with the CRC generator ; moreover, to preserve error detection capability, CRC generator polynomial shall have no common factors with scrambler polynomial. All standard CRC-16 polynomial have x + 1 as a factor which is also a factor in x^43^ + 1 ; a new CRC-16 was required that preserved error detecting capability. The syndrome for single error and double errors spaced 43 bits '''must''' all be unique."

Performance of a cyclic redundancy check and its interaction with a data scrambler, IBM

Script de génération des équations parallèles.

Le script en perl crcgen.pl permet de générer les équations parallèles d'un calcul de crc et de syndrome pour une taille de bus et un polynome générateur paramètrable. Le coeur du script comporte deux parties, l'une calcul les équations pour chaque itération de la taille du bus, l'autre optimise ces équations. Le générateur d'équations parallèles crc et syndrome différe simplement par la contre réaction.

Il était une fois ... Les codes correcteurs d'erreurs.

Liens externes & documentation.

Error Control Coding (ECC), Shu Lin & Daniel J. Costello, Chapter 5 Cyclic codes p136.
The art of error correcting coding (Wiley), Robert H. Morelos-Zaragoza.

Xilinx application note IEE802.3 and CRC
Web CRC tools
Un brevet...
Pojet Opencores.

Glossaire.

CRC       Cyclic Redundancy Check
ECC       Error Checking Code
g(x)      generator polynomial
h(x)      Parity check polynomial
i(x)      information polynomial
c(x)      transmit code polynomial
r(x)      receive code polynomial
e(x)      error polynomial
s(x)      syndrome polynomial