Partie A - Encodeur Reed-Solomon.

1 - Introduction et définitions.

2 - Polynôme générateur et polynôme primitif.

3 - Corps finis de Galois et arithmétique.

4 - Coefficients du polynôme générateur.

5 - Encodeur RS.

6 - Introduction au décodeur RS.

7 - Liens & documentation.

Partie A.1 - Introduction et définitions.

Ces codes correcteurs d'erreurs (CCE) sont utilisés dans les technologies de transmission de l'information ou dans l'aérospatiale. Les CCE peuvent être divisés en deux grandes familles : codes en blocs ou codes récurrents. Dans la deuxième famille, qui sont des codes séquentiels ou convolutif, un effet de mémoire est introduit, cela sera l'objet d'un autre article (codage Viterbi).
Les symboles appartiennent à un alphabet de q éléments, ils seront dits q-aires (binaire, ternaire, quartet, octet...) selon la valeur de q. Dans le cas qui nous interesse, q vaudra 8 : ce sont des octets. On appelle code en bloc (ou block code) un code ou les symboles issues de la source (information) sont regroupés par blocs de k. Dans le cas de la TnT k est un bloc de 188 octets issue du transport stream MPEG, dans les télécommunication CWDM (trame OTN G709) k sera une décomposition d'une ligne de la trame et vaudra 239 octets. 'n' correspondra à la taille du bloc après codage, n sera supérieur à k afin de satisfaire la condition de redondance. n-k correspondra donc au nombre de symbole de parité ajouté par le codeur et vaudra 16 pour les deux exemples cités plus haut. Le code est dit systématique si les k premiers symboles du bloc encodé sont égaux aux symboles du bloc d'information. Le rendement d'un code C(n,k) vaut R = k/n.
Le poids de Hamming d'un mot est le nombre de bits à 1 qu'il contient. La distance de Hamming entre deux mots de même longueur est définie par le nombre de positions binaires qui diffèrent entre ces deux mots. On l'obtient par le poids de Hamming de la somme binaire des 2 mots. La distance de Hamming d'un code est la distance minimum entre tous les mots du code. Si d_min est la distance minimale de hamming d'un code, il est possible de montrer que le nombre maximum d'erreurs corrigibles est t = (dmin - 1)/2.

Figure 1 : Reed-solomon Encoder block diagramm.

www.opencores.org propose les sources d'un codeur RS, au format Verilog peu clair et sans aucune explication. Quelques autres sources diffusent des informations soient pertinentes, soit erronées. Remédions à cet état de fait et expliquons en "succinctement" le principe.

Partie A.2 - Polynôme générateur et polynôme primitif..

L'arithmétique des champs finis fut découverte par Evarsite Galois (1811 Bourg-la Reine, 1832). Un corps de Galois est un ensemble pour lequel le résultat de certaines opérations arithmétiques (addition, multiplication...) entre deux éléments du corps est un autre élément du corps.
Un polynôme primitif p(x) est utilisé pour définir les éléments du corps de Galois GF ; à chaque largeur de symbole correspond quelques polynômes primitifs valident de degré n pour un symbole de n bits. Dans le cas d'un traitement au niveau octet le polynôme utilisé est :

p(x) = x^8 + x^4 + x^3 + x^2 + 1
ou encore : p(x) = 1 0 1 1 1 0 0 0 1 (1+x^2+x^3+x^4+x^8) soit p(x) = 285 utilisé

Le polynome générateur g(x) permet quant à lui de générer les octets appropriés de parité pour chaque block de k symbole d'information. g(x) est de degré n-k et vaut dans le cas de la TnT ou tout autre système ajoutant 16 octets de parité :

g(x) = (x + α⁰).(x + α¹). ... .(x + α¹⁵)

g(x) = Produit de i=b à b+n-k-1 (x - αⁱ)

Partie A.3 - Corps finis de Galois et arithmétique.

La clef de voûte pour la compréhension d'un codec Reed-Solomon, c'est le corps de Galois. L'analyse détaillée des corps finis sort largement du cadre de cet exposé, le lecteur intéressé par la théorie mathématique se reportera à un ouvrage spécialisé. Il est toutefois nécessaire d'appréhender quelques notions afin de comprendre le principe des codes cycliques. Quelques aspects vont être abordés : la génération des éléments de GF ainsi que certains opérations arithmétiques sur le Corps de Galois, puis le principe de génération des coefficients du polynôme générateur.

Un corps finis est une structure algébrique mathématique très utile dans laquelle il est possible d'additionner, soustraire, multiplier ou diviser et ce sur des nombres réels ou complexes. Un champs à q éléments sera noté GF(p) ; par exemple GF(2) est composé de deux éléments {0,1}. Par extension, nous noterons GF(p^m) un champs fini dans lequel le nombre d'élément est une puissance entière d'un nombre premier p. Pour p=2, dans le champs GF(2^m) il existe toujours un élément primitif α qui permet d'exprimer tout élément de GF(2^m) sauf zéro comme une puissance de α. Il est possible de générer n'importe quel corps GF(2^m) en utilisant un polynôme primitif sur GF(2) ; l'arithmétique effectuée dans le champs GF(2^m) est le modulo du polynôme primitif.

Regardons le cas plus concret de GF(2³) ; le polynôme primitif de degré 3 que l'on peut utiliser pour générer les éléments de GF(2³) est donné par p(x) = x³ + x + 1. Prenons α un élément primitif de GF(2³) ; comme α est une racine de p(x), α³ + α + 1 = 0 et selon certaines propriétés α³ = α + 1. Maintenant, appliquons ces résultats et propriétés afin de générer tous les éléments du champs GF(2³) en terme de puissance de α.

Table 2 : Valeur des éléments du champs GF(2³).

Notation exponentielle	notation polynomiale	Notation binaire A(i)	table log L(i)
0 ou α7	0	000	5
α0	1	001	-1
α1	X	010	0
α2	X2	100	1
α3=α1+1	X + 1	011	3
α4	X2+ X	110	2
α5=α3+α2	X2 + X + 1	111	6
α6=α2+1	X2 + 1	101	4

La représentation polynomiale des éléments du champs facilite les opérations mathématiques ; une addition de deux éléments du champs consistera à additionner les coefficients du polynome primitif : par exemple ajouter α² à α³ consiste à ajouter modulo 2 les valeurs 100 et 011 soit 111 = α⁵. La multiplication de deux éléments du champs s'effectue en ajoutant les puissances de α modulo 2^m-1 (soit 7 dans notre cas ou m vaut 3). Par exemple, α ⁴ par α⁶ vaudra α^10mod(7) soit α³.

Il est d'usage d'utiliser deux tables, l'une anti-log A(i) permet d'effectuer des additions. Cette table retourne la valeur binaire d'une puiisance de alpha. La seconde table appelée log ou L(i) permet de réaliser les multiplications, cette table retourne la puissance de alpha d'un vecteur.

Avant de s'atteler au cas le plus traditionnel GF(2⁸) regardons GF(2⁴) = GF(16) et qui comprend donc 15 éléments notés de α0 à α14. Un polynome primitif valide est p(x) = x⁴ + x + 1 = 10011. α est racine de p(x) (Ceci n'est pas démontré ici mais est analogue au nombre imaginaire 'i' racine de l'équation x^2 + 1 = 0).

Table 3 : Valeur des éléments du champs GF(2⁴).

Notation exponentielle	0	α0	α1	α2	α3	α4	α5	α6	α7	α8	α9	α10	α11	α12	α13	α14
Notation binaire	0000	0001	0010	0100	1000	0011	0110	1100	1011	0101	1010	0111	1110	1111	1101	1001

Notons que la somme α⁴ + α + 1 vaut zéro et que α est donc bien une racine de p(x). La représentation des éléments du corps de Galois correspond à l'interprétation des coefficients d'un polynôme de degré 3. L'identité α⁴ + α + 1 = 0 permet de ramener les exposants à la valeur maximale de trois.

Algorithme de génération de GF(2^8).
p(x) = x^8 + x^4 + x^3 + x^2 + 1
coef : 8 7654 3210
p(x) = 1 0001 1101

  a0 = 0 0000 0001 initialisation
  a1 = 0 0000 0010 ROL (ROtate Left)
  ...
  a6 = 0 0100 0000 ROL
  a7 = 0 1000 0000 ROL
  a8 = 1 0000 0000 ROL C=1
     + 1 0001 1101 donc normalisation
  a8 = 0 0001 1101
  a9 = 0 0011 1010 ROL
 a10 = 0 0111 0100 ROL
 a11 = 0 1110 1000
 a12 = 1 1101 0000 ROL C=1
     + 1 0001 1101
 a12 = 0 1100 1101
 a13 = 1 1001 1010
     + 1 0001 1101
 a13 = 0 1000 0111

poly_prim = 1 0001 1101; -- initialisation
alpha_to[0] = 1; -- initialisation
pour (i=1 i inférieur à 255 i++) -- boucle sur les éléments de CG
  alpha_to[i] ROL alpha_to[i-1]; -- décalage à gauche de n-1
  if (MSB de alpha_to[i] = 1) --  test de x^8
    alpha_to[i] = alpha_to[i] xor poly_prim; -- normalisation
  fin si
fin pour

Regardons de plus près la multiplication. C'est la somme des puissances de α modulo 2^m-1 Cette formule bien pratique pour l'informaticien s'avère difficilement utilisable pour l'électronicien. Cherchons donc les équations littérales de la multiplication simple pour commencer avec des symboles de type quartet.
Soit A et B deux éléments de GF(16) :

A = a3.α³ + a2.α² + a1.α + a0
B = b3.α³ + b2.α² + b1.α + b0

A.B =
(a3.b3)α⁶ +
(a3.b2 + a2.b3)α⁵ +
(a3.b1 + a2.b2 + a1.b3)α⁴ +
(a3.b0 + a2.b1 + a1.b2 + a0.b3)α³ +
(a2.b0 + a1.b1 + a0.b2)α² +
(a1.b0 + a0.b1)α¹ +
(a0.b0)

Ce résultat présente sept coefficients que nous devons convertir en 4-aires (quartet); pour cela nous substituerons α⁶, α⁵ et α⁴ par leur représentation polynomiale. (soit respectivement x^3+x^2, x^2+x et x+1).

A.B =
(a3.b3 + a3.b0 + a2.b1 + a1.b2 + a0.b3)α³ +
(a3.b3 + a3.b2 + a2.b3 + a2.b0 + a1.b1 + a0.b2)α² +
(a3.b1 + a2.b2 + a1.b3 + a1.b0 + a3.b2 + a2.b3 + a0.b1)α¹ +
(a3.b1 + a2.b2 + a1.b3 + a0.b0)

Les performances d'un codeur/décodeur Reed Solomon dépendent en partie de l'arithmétique des corps finis (field). Si l'addition est simple et consiste uniquement en un ou exclusif des éléments des symboles, il en va tout autrement du multiplieur. Différentes structures ont été développées :

• Linear Feedback Shift Register multiplier (LFSR).
• Mastrovito multiplier.
• Massey-Omura multiplier.
• Hasan-Ghargava multiplier.
• Paar-Rosner multiplier
• Morii-Berlekamp multiplier.
• Pipelined combinatorial multiplier.

Partie A.4 - Coefficients du polynôme générateur.

Pour calculer les symboles de parité, il faut connaître les coefficients du polynôme générateur. Intéressons nous au code RS(7,3,5) dans GF(2^3) ou p(x) = x^3 + x + 1 est polynome primitif, donc p(α) = α³ +α + 1 = 0 et donc :

g(x) = produit de i=0 à n-k-1 (x + αⁱ)
g(x) = (x + 1).(x + α¹).(x + α²).(x + α³)

Soit après addition des notations binaires associées de la table 2 :

g(x) = x^4 + α².x^3 + α⁵.x^2 + α⁵.x + α⁶

g(x) = x^6 + α¹².x^5 + x^4 + α².x^3 + α⁷.x^2 + α¹¹.x + α⁶

Le calcul manuel des autres coefficients est fastidieux, il vaut mieux utiliser un algorithme en C par exemple. Rappelons tout d'abords le triangle de Pascal qui permet de calculer les coefficients du développement de (x+1)^n

 (x+1)^0 : 0 : 1
 (x+1)^1 : 1 : 1 1
 (x+1)^2 : 2 : 1 2 1
 (x+1)^3 : 3 : 1 3 3 1
 (x+1)^4 : 4 : 1 4 6 4 1

for (ligne = 1; ligne <= red; ligne++) {
  tab_coef[ligne] = 1;
  for (colonne = ligne-1; colonne > 0; colonne--)
    tab_coef[colonne] = tab_coef[colonne-1] + tab_coef[colonne];
   fin pour;
fin pour;

0 : 1
1 : 1=a : 0+1.α⁰=b
2 : 1=c : b+a.α¹=d : 0+b.α¹=e
3 : 1=f : d+c.α²=g : e+d.α²=h : 0+e.α²=i

tab_coef[c] = α^ligne-1.tab_coef[c-1] + tab_coef[c];
La multiplication est réalisée en aditionnant modulo 2^m les puissances de alpha.
L'addition est le ou exclusif des formes vectorielles.

// colonne(i) = colonne(i-1).A^(ligne-1) xor colonne(i)
// Note1 : index_of(vector) retourne la puissance de alpha. 
//         exemple : index_of(6) retourne 4
// Note2 : pour effectuer la multiplication prendre la puissance de alpha
//         de colonne(i-1) puis appliquer la relation :
//         alpha^i.alpha^j = alpha(i+j)modulo(2^m)
// Note3 : pour effectuer le xor : prendre index_of(valeur) afin de calculer
//         sur les valeurs décimales.
// Le résultat obtenu sera sous forme décimale. (vector)
// Nous trouvons par calcul et pour une valeur initiale b=0 puis b=1 :

gin(0)  =  59 pour b=0,  79 pour b=1
gin(1)  =  36 pour b=0,  44 pour b=1
gin(2)  =  50 pour b=0,  81 pour b=1
gin(3)  =  98 pour b=0, 100 pour b=1
gin(4)  = 229 pour b=0,  49 pour b=1
gin(5)  =  41 pour b=0, 183 pour b=1
gin(6)  =  65 pour b=0,  56 pour b=1
gin(7)  = 163 pour b=0,  17 pour b=1
gin(8)  =   8 pour b=0, 232 pour b=1
gin(9)  =  30 pour b=0, 187 pour b=1
gin(10) = 209 pour b=0, 126 pour b=1
gin(11) =  68 pour b=0, 104 pour b=1
gin(12) = 189 pour b=0,  31 pour b=1
gin(13) = 104 pour b=0, 103 pour b=1
gin(14) =  13 pour b=0,  52 pour b=1
gin(15) =  59 pour b=0, 118 pour b=1

Partie A.5 - Encodeur Reed-Solomon.

Le code RS utilisé pour la TNT permet de corriger 8 octets erronés par paquet de transport. Ce mécanisme ajoute donc 16 octets de redondance au paquet initial afin d'obtenir un mot de code (204,188,8) : (n,k,t). Ce mécanisme peut corriger jusqu'à 8 symboles, c'est un code adapté pour corriger les erreurs en rafale (burst) introduites par le canal de transmission (voies hertziennes terrestres). Le code (204,188,8) est une version raccourcie de (255,239,8) qu'il est possible d'utiliser en ajoutant 51 octets nuls avant les 188 d'information. En sortie de codeur, les octets nuls sont supprimés le code bloc étant ainsi ramené aux 204 symboles utiles.

Revenons à l'encodage Reed-solomon.
En général, pour un code Reed-Solomon, le polynome g(x) est de la forme :

g(x) = (x - λ^b) + (x - λ^b+1) + ... + (x - λ^b+2t-1)

p(x) = i(x) . x^(n-k) + [i(x) . x^(n-k)]. mod g(x)

Figure 2 : Reed-Solomon Encoder block diagramm.

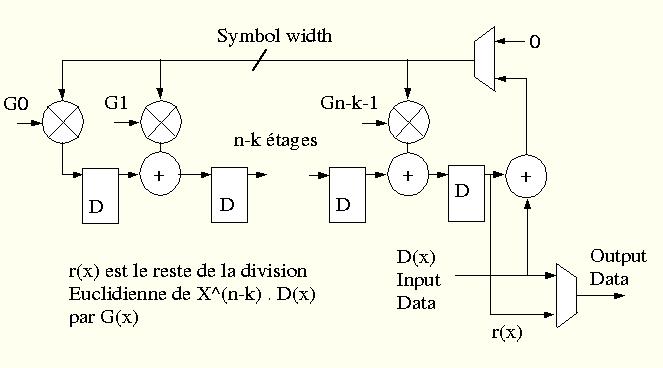
Code source vhdl de l'encodeur RS au format html.
Code source vhdl de l'encodeur RS au format vhdl.
Code source en C de cacul des coefficients du polynome générateur.

Partie A.6 - Introduction au décodeur RS..

Le décodage, très demandeur en ressources, est basé sur l'algorithme Peterson-Gorenstein- Zierler qui utilise des calculs matriciels ; la procédure consiste à déterminer la localisation des erreurs (les puissances de X) dans le polynome reçu, ainsi que l'amplitude de l'erreur (le symbole qu'il faudrait ajouter au symbole reçu afin de retrouver le symbole encoder d'origine). Le polynome d'erreur e(x) s'écrit :

e(x) = e_i1.x⁽ⁱ¹⁾ + e_i2.x⁽ⁱ²⁾ + ... + e_iv.x^(iv)

Figure 2 : Calcul du syndrome.

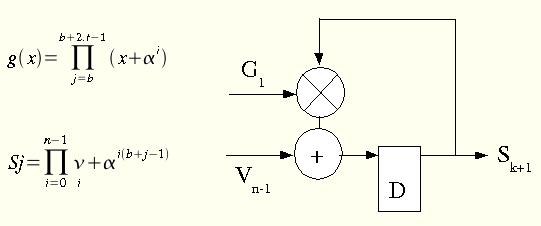
Le syndrome consiste à l'évaluation de r(x), mot reçu, pour chaque zéro du code (α puissance i, racine du polynome générateur). le mot reçu r(x) correspond à la somme du mot transmis v(x) plus l'erreur e(x) apportée par le canal de transmission.

S1 = r(α^b)
S2 = r(α^b+1)...
r(x) = v(x) + e(x)

Partie A.7 - Liens & documentation.

Compiler un source avec gcc :
cc new2_rs_erasures.c -DNO_PRINT -lm -o rsgp
cc rs_cal.c -o rs_cal

Programmes en C (new_rs_erasures.c)
Introduction aux CCE : article de RF design magazine.
part 1: Viterbi codecs.(edn magazine, web)
part 2: Reed-Solomon codecs.(edn magazine, web)
Partie 1 : codeurs Viterbi.(pdf local)
Partie 2 : Reed-Solomon codecs.(pdf local)
Reed-Solomon Codec Design in Programmable Logic.
Projet RScode de sourceforge.net (utilisé pour les CD).
Projet encodeur RS de opencores. (foireux, à éviter)
Codes linéaires, codes cycliques, corps de Galois. (par Pierre Csillag)
Corps de Galois, aide mémoire de A. Le Glaunec (pdf local)
Architecture d'un multiplieur ds GF ; source : IEEE. (pdf local)
Multiplieur dans le corps de Galois. (article IEEE)

Pour terminer cette première partie, les sources permettant de simuler l'encodeur ainsi que la vérification par calcul du syndrome. Les heureux propriétaires de Core-generator (outil xilinx) pourront corréler les résultats fournis par le core avec ceux du code proposé, les autres se contenteront du syndrome... Le fichier (format zip) contient le testbench ainsi que les différents composants, une macro de commande ModelSim et les signaux à visualiser ; pour l'utiliser, créer un projet avec les fichiers puis >Tools>Execute Macro/commande_tnt.do
Sources vhdl, testbench et macro model sim. (version du 1 juin 2005)

Interprétation et analyse :
La véracité de la fonction de multiplication dans le corps est facile à valider, il suffit de vérifier avec la formule mathématique (somme des puissances de alpha modulo 255) que l'on retrouve le même résultat. Pour les coefficient le core xilinx confirme les valeurs : pour cela utiliser le pattern spécifique ou toute la charge est nulle sauf le dernier symbole à 01 : dans ce cas (et sans insertion d'erreur), les symbole de redondance correspondent aux racines du polynome générateur. (la fonction de multiplication n'est pas réellement utilisée). Au-delà, cela se complique, il faut corréler avec une source fiable.

The art of error coding,
Robert Morelos-Zaragoza,
Wiley

Pierre Csillag
Introduction aux Codes Correcteurs
Ellipses, Paris, 1990

Autres livres techniques sur les codes correcteurs d'erreurs.
Librairie scientifique et technique Lavoisier.

BCH : Bose-Chaudhuri-Hockenghem.
BMA : Berlekamp-Massey-Algorithm.
EA : Euclid-Algorithm.
ECC/CCE : Code Correcteur d'erreurs.
FEC : Forward Error Coding.
GF(n) : Galois Fields, champs de Galois.
TNT : Télévision Numérique Terrestre.
SPDIF : Sony/Philips Digital Interface. Transfert de données audio stéréo.
I2S : Serial Digital audio bus.
VGA : Voltage Gain Amplifier. Amplificateur à gain variable.
CVBS : Composite Video Vand Vignal.
Y-C : Luminance/Chrominance.
DVB : Digital Video Broadcasting. (Télévision numérique.)
DVB-C : DVB Cable.
DVB-S : DVB Satellite.
DVB-T : DVB Terrestre.
COFDM : Coded hOrthogonal Frequency Division Multiplex.

Plan de la rubrique électronique.
Les techniques de la TnT.